《2025年学霸甘肃少年儿童出版社五年级数学上册苏教版》

8. 小军有x本科普书,小刚的科普书的本数是小军的7倍。
(1)$7x$表示(小刚的科普书的本数)。
(2)$7x + x$表示(小军和小刚的科普书的总本数)。
(3)$7x - x$表示(小刚比小军多的科普书的本数(合理即可))。

答案： 8.
(1)小刚的科普书的本数
(2)小军和小刚的科普书的总本数
(3)小刚比小军多的科普书的本数(合理即可)

9.

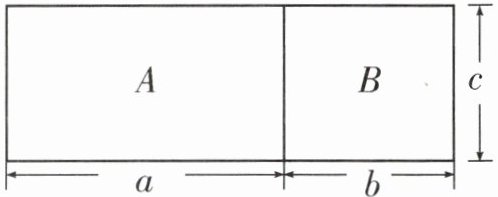
(1)长方形A的周长是(2(a+c)),面积是(ac)。
(2)长方形B的周长是(2(b+c)),面积是(bc)。
(3)整个图形的周长是(2(a+b+c)),面积是((a+b)c)。

答案： 9.
(1)2(a+c) ac
(2)2(b+c) bc
(3)2(a+b+c) (a+b)c

10. 找规律填空。
(1)2.3,4.5,6.7,8.9,…,m,(m+2.2)。
(2)第n个数是多少？
0,3,8,15,24,…,(n²-1)……
(3)2² - 1² = 3
3² - 2² = 5
4² - 3² = 7
5² - 4² = 9
…
10² - (9²) = (19)
…
n² - ((n-1)²) = (2n-1)

答案： 10.
(1)m+2.2
(2)$ n^{2}-1 $
(3)$ 9^{2} $ 19 $ (n-1)^{2} $ 2n-1

11. 黑、白棋子按一层白、一层黑排成等边三角形的形状,如图。

当一个等边三角形中黑棋子比白棋子多n颗时,这个等边三角形一共排了(2n)层。

答案： 11. 2n

12. 对一个整数进行下列操作：如果它是单数,把这个数加上3；如果它是双数,把这个数除以2。若这个数是11,第1次操作的结果是14,第2次操作的结果是7,第3次操作的结果是10……依次操作,第2025次操作的结果是(4)。

答案： 12. 4 提示:10÷2=5,5+3=8,8÷2=4,4÷2=2,2÷2=1,1+3=4,可知操作结果依次为14、7、10、5、8、4、2、1、4、2、1……从第6次操作开始，出现以4、2、1为一个周期的循环,(2025-5)÷3的余数为1,则第2025次操作的结果是4。

13. 根据下面图形的排列规律,用含有字母n的式子表示B和C的值。

答案： 13. B=2n-1 C=(3n-2)n 提示:观察方格中的数可以发现，每一组方格中的4个数，左下角的数是上面两个数的和，右下角的数是左列两个数的和与右上角数的积。所以B=(n-1)+n=2n-1,C=(n-1+2n-1)n=(3n-2)n。

14. 把1、3、6、10、15……这些数叫作三角形数,因为这些数目的点可以排成一个等边三角形(如图)。

按照这样的规律：第10个三角形数是(55),第n个三角形数是((1+n)n÷2)。

答案： 14. 55 (1+n)n÷2 提示:通过观察可以发现，每个三角形数都是由三角形中每行上的点数相加得到的。第10个三角形数是1+2+3+4+…+10=(1+10)×10÷2=55,第n个三角形数是1+2+3+4+…+n=(1+n)n÷2。