《2025年学霸甘肃少年儿童出版社五年级数学上册苏教版》

8. 明明(男)、亮亮(男)、晶晶(女)、莹莹(女)四个好朋友在拍合影照片。
(1)如果他们站在一排拍合影照片,一共有(24)种不同的站法;如果亮亮站在左起第三位,一共有(6)种不同的站法。
(2)如果他们站在一排拍合影照片,要求男女间隔排列,一共有(8)种不同的站法。
(3)如果他们站成两排拍合影照片,前一排站一人,后一排站三人,一共有(24)种不同的站法。

答案：
(1)24 6
(2)8
(3)24

9. 五(2)班部分同学和家长共48人,在两位老师的带领下到公园去划船。已知每条小船可以坐4人,每条大船可以坐6人,大船和小船都要坐满人。租大、小船有多少种不同的方案?如果每条大船的租金是20元,每条小船的租金是15元,怎样租船最合算? 最少要花多少钱

答案：
有4种方案,如下表所示:

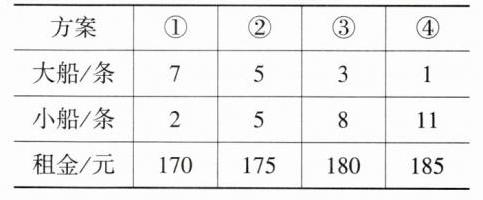
租7条大船、2条小船最合算,最少要花170元。

10. 李大伯要用20根1米长的栅栏围一个长方形的羊圈,其中一面靠墙(墙足够长,长、宽均为整数),有多少种不同的围法? 怎样围的面积最大?

答案： 9种 当长10米,宽5米时,面积最大

11. 王明买了6张电影票(如图),他想把4张票连在一起撕下,共有几种不同的方法$?\begin{tabular}{|c|c|c|}\hline 1 & 2 & 3 \\\hline 4 & 5 & 6 \\\hline\end{tabular}\\\hline $

答案： 3+3+4=10(种)

12. 一列火车在上海与南京之间往返行驶,中间停靠苏州、无锡和常州,每两地之间路程都不相同,铁路局应准备多少种不同的火车票?(在相同的两站往返的车票是不同的)

答案： (4+3+2+1)×2=20(种) 提示:根据题意,可以画出下面的线段图。我们可以采用数线段的方法。上海到南京方向,一共要准备4+3+2+1=10(种)不同的车票;同样,南京到上海方向,也要准备10种不同的车票。所以铁路局应准备20种不同的火车票。
常州 南京 上海 苏州 无锡

13. 从分别写着1、2、3、4、5、6、7、8的八张卡片中取两张写出一道一位数的加法题,一共有多少道不同的算式(如果加数只有顺序不同,算一道算式)? 一共有几种不同的和?

答案： 7+6+5+4+3+2+1=28(道) 15 - 3 + 1 = 13(种) 提示:1与其他7个数能组成7道,2与比它大的其他6个数能组成6道,3与比它大的其他5个数能组成5道,4与比它大的其他4个数能组成4道,5与比它大的其他3个数能组成3道,6与比它大的其他2个数能组成2道,7和8组成1道。列式:7+6+5+4+3+2+1=28(道)。在所有算式中,最小的和是1+2=3,最大的和是7+8=15,所以和一共有15 - 3 + 1 = 13(种)。

14. 有一张表,写有1~500的所有自然数。在这张表里数字“5”共出现多少次?

答案： 50+50+1=101(次) 提示:个位上有50个5,十位上有50个5,百位上有1个5,所以“5”共出现50+50+1=101(次)。我们还可以这样分类考虑:一位数中,出现数字“5”的数:5,1次;两位数中,出现数字“5”的数:15、25、35、45、50、51、52、53、54、55、56、57、58、59、65、75、85、95,其中55出现2次5,共19次,则在1~99中数字“5”共出现了20次。同理,100~199,200~299,300~399和400~499中出现数字“5”的次数与1~99中数字“5”出现的次数一样多。那么数字“5”一共出现的次数为20×5+1=101(次)。