《2025年学霸甘肃少年儿童出版社五年级数学上册苏教版》

1. 人文历史 素有“天下第一桥”之称的赵州桥是由若干个梯形石块搭建而成的拱桥。如图,一块用于搭建拱桥的长方形石块按如图方式加工成梯形后,面积减少了(3)平方分米。

答案： 3 提示:方法一:梯形的面积为$(3 + 5)×3÷2 = 12$(平方分米)，长方形的面积为$5×3 = 15$(平方分米)，则减少的面积为$15 - 12 = 3$(平方分米)。方法二:减少的面积=两个三角形面积的和=$(5 - 3)×3÷2 = 3$(平方分米)。

2. 热点视窗 2024年11月中旬为期6天的珠海航展,总参观人数近60万,展品数量创历史新高,每一项展品都凝聚着科技与智慧的结晶,彰显了大国崛起的非凡气势。乐乐在参观完航展后,按照中国航天的标志画出一个图形,如图。图中涂色部分的面积是(60)平方厘米。

答案： 60 提示:涂色部分的面积=大三角形的面积 - 小三角形的面积=$12×16÷2 - 12×6÷2 = 60$(平方厘米)。

3. 算理理解

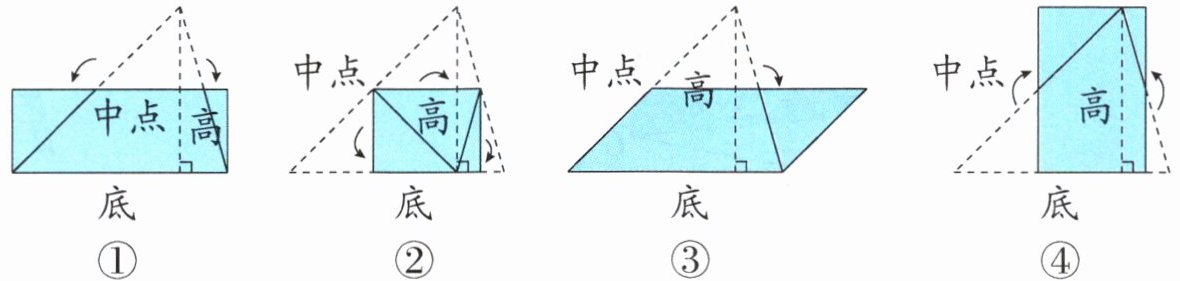
(1)上面几种推导三角形面积计算公式的方法中,正确的有(4)种。
(2)图①的推导过程中,没有用到的是(C)。
A. 割补法 B. 转化的策略 C. 长方形的周长公式 D. 长方形的面积公式
(3)图②中折成的长方形长为7厘米,宽为4厘米,则原来这个三角形的面积是(56)平方厘米。

答案：
(1)4 提示:题图①将三角形剪拼成一个长方形，三角形的面积与长方形的面积相等，长方形的底相当于三角形的底，长方形的高相当于三角形的高的一半，所以三角形的面积=长方形的面积=长×宽=底×(高÷2)=底×高÷2。题图②是将三角形折成一个长方形，三角形的面积是这个长方形面积的 2 倍。长方形的长相当于三角形底的一半，长方形的宽相当于三角形高的一半，因为长方形的面积=长×宽，所以三角形的面积=(底÷2)×(高÷2)×2 = 底×高÷2。题图③是将三角形剪拼成一个平行四边形，三角形的面积与平行四边形的面积相等。平行四边形的底相当于三角形的底，平行四边形的高相当于三角形高的一半，所以三角形的面积=平行四边形的面积=底×(高÷2)=底×高÷2。题图④同理可得，三角形的面积=长方形的面积=(底÷2)×高=底×高÷2。所以这几种推导三角形面积公式的方法中，正确的有 4 种。
(2)C 提示:观察题图可知，用割补法将三角形转化成一个长方形，转化后的长方形的面积等于三角形的面积，长方形的长相当于三角形的底，长方形的宽相当于三角形高的一半。因此推导过程用到了 ABD，没有用到 C。
(3)56 提示:由题图可知，原来三角形的面积是长方形面积的 2 倍，因此原来三角形的面积=$7×4×2 = 56$(平方厘米)。

4. 推导探究 如图①,在三角形ABC中,D是边AB的中点,可知AD= BD,则三角形BCD与三角形ACD的面积相等。

(1)如图②,在三角形ABC中,D、E分别是AB和AC两边的中点。已知三角形ADE的面积是2平方厘米,则三角形ABC的面积是(8)平方厘米。
(2)如图③,在三角形ABC中,把AB边三等分、AC边四等分。已知三角形ADE的面积是2平方厘米,则三角形ABC的面积是(24)平方厘米。
(3)如图④,在平行四边形ABCD中,把AB边五等分、AD边六等分。已知平行四边形ABCD的面积是60平方厘米,则三角形AEF的面积是(1)平方厘米。

答案：
(1)8
(2)24
(3)1 提示:
(1)因为 E 是 AC 边的中点，所以三角形 ADE 的面积=三角形 CDE 的面积；因为 D 是 AB 边的中点，所以三角形 BCD 的面积=三角形 ACD 的面积。所以三角形 ACD 的面积=三角形 ADE 的面积×2=$2×2 = 4$(平方厘米)，三角形 ABC 的面积=三角形 ACD 的面积×2=$4×2 = 8$(平方厘米)。
(2)连接 CD，因为把 AC 边四等分，所以三角形 ACD 的面积=三角形 ADE 的面积×4=$2×4 = 8$(平方厘米)。因为把 AB 边三等分，所以三角形 ABC 的面积=三角形 ACD 的面积×3=$8×3 = 24$(平方厘米)。
(3)连接 BD、DE，因为三角形 ABD 的面积=平行四边形的面积÷2=$60÷2 = 30$(平方厘米)，三角形 ADE 的面积=三角形 ABD 的面积÷5=$30÷5 = 6$(平方厘米)，所以三角形 AEF 的面积=三角形 ADE 的面积÷6=$6÷6 = 1$(平方厘米)。