《2025年学霸甘肃少年儿童出版社五年级数学上册苏教版》

例1 下图中有多少个正方形包含“☆”？

分析：把每个小正方形的边长看作1,边长为1且包含“☆”的正方形有1个,边长为2且包含“☆”的正方形有4个,边长为3且包含“☆”的正方形有6个,边长为4且包含“☆”的正方形有3个,这样可求出包含“☆”的正方形的总个数。
解答：$1 + 4 + 6 + 3 = 14$(个)

答案： 边长为1且包含“☆”的正方形：1个
边长为2且包含“☆”的正方形：4个
边长为3且包含“☆”的正方形：6个
边长为4且包含“☆”的正方形：4个
边长为5且包含“☆”的正方形：1个
总个数：1+4+6+4+1=16（个）

1. 将一个非零自然数拆分成若干个小于它的非零自然数之和,例如：$3 = 1 + 2$,$3 = 1 + 1 + 1$。如果加数只有顺序不同,算一种拆分,那么6一共有多少种不同的拆法？(加数不可为0)

答案： 10种　提示:可以从拆成两个数的和想起。两个数的和:6=1+5=2+4=3+3;三个数的和:6=1+1+4=1+2+3=2+2+2;四个数的和:6=1+1+1+3=1+1+2+2;五个数的和:6=1+1+1+1+2;六个数的和:6=1+1+1+1+1+1。可见一共有10种不同的拆法。

2. $□ - ◯ = \triangle$的减法算式中,每个图形代表的数字是1,2,3,…,9中的一个且各不相同。你能列出多少种不同的算式？

答案： 32种　提示:□=9,可以写出8种不同的算式，□=8,可以写出6种不同的算式……□=4,可以写出2种不同的算式，□=3,可以写出2种不同的算式。所以一共可以写出8+6+6+4+4+2+2=32(种)不同的算式。

3. 有10对夫妇共20人参加一次元旦晚会,其中每位男宾与其他每一个人握一次手(他的夫人除外),女宾与女宾不握手,晚会上这20个人之间一共互相握了(135)次手。

答案： 135　提示:从男宾入手，第一个男宾握手18次，第二个男宾不再与第一个男宾握手，还要握手17次，第三个男宾不再与前面两个男宾握手，还要握手16次……第十个男宾与九个女宾握手，还要握手9次。则一共握手的次数为18+17+16+...+10+9=135(次)。

例2 甲、乙两人打乒乓球,谁先连胜头两局谁赢,如果没有人连胜头两局,则谁先胜三局谁赢,决出胜负共有多少种可能呢？(不考虑平局)
分析：这题可通过画图来解答。

图中从上至下每一条路径表示有一种可能。例如,最左边一条路径：甲—甲就表示甲连胜头两局,甲赢的一种可能。最右边一条路径：甲—乙—乙—乙表示甲胜第一局,接着乙胜了三局,乙赢的一种可能。因此,第一局甲赢,决出胜负 有7种可能。同理,如果第一局乙赢,决出胜负也有7种可能。
解答：$7 + 7 = 14$(种)

答案： 第一局甲赢的情况：
甲连胜两局：甲、甲（1种）
甲赢第一局，乙赢第二局后：
甲赢第三局，甲赢第四局：甲、乙、甲、甲（1种）
甲赢第三局，乙赢第四局，甲赢第五局：甲、乙、甲、乙、甲（1种）
甲赢第三局，乙赢第四局，乙赢第五局：甲、乙、甲、乙、乙（1种）
乙赢第三局，乙赢第四局：甲、乙、乙、乙（1种）
乙赢第三局，甲赢第四局，甲赢第五局：甲、乙、乙、甲、甲（1种）
乙赢第三局，甲赢第四局，乙赢第五局：甲、乙、乙、甲、乙（1种）
共7种。
第一局乙赢的情况同理也有7种。
总共有：7+7=14（种）
答：决出胜负共有14种可能。

4. 甲、乙两人进行围棋比赛(比赛实行七局四胜制),规定先胜四局者胜,第一、二局甲胜,第三局乙胜。最后决出胜负,可能有几种情况？其中甲胜出的情况有几种？

答案：
共有10种情况，其中甲胜出的情况有6种。提示: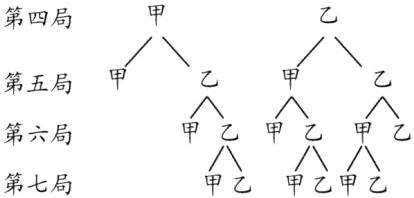 由图可知，一共有10种情况，其中甲胜出的情况有6种。