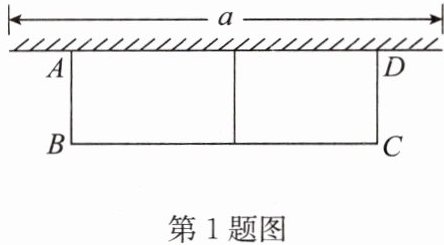
1. 如图,有长为 24 米的篱笆,一面利用墙(墙的最大可用长度 a 为 15 米)围成中间隔有一道篱笆的长方形花圃. 设花圃的宽 AB 为 x 米,面积为 S.
(1)求 S 与 x 的函数关系式;
(2)当 AB 的长为多少时,花圃的面积最大? 最大值是多少?
(1)求 S 与 x 的函数关系式;
(2)当 AB 的长为多少时,花圃的面积最大? 最大值是多少?

答案:
1.解:
(1)
∵花圃的宽AB为x米,篱笆长为24米,
∴BC=(24-3x)米,
∴S=x(24-3x)=-3x²+24x(3≤x<8).
∴S与x的函数关系式为S=-3x²+24x(3≤x<8).
(2)S=-3x²+24x=-3(x-4)²+48.
∵3≤x<8,
∴当x=4时,S有最大值,最大值为48.
答:当AB的长为4米时,花圃的面积最大,最大值是48平方米.
(1)
∵花圃的宽AB为x米,篱笆长为24米,
∴BC=(24-3x)米,
∴S=x(24-3x)=-3x²+24x(3≤x<8).
∴S与x的函数关系式为S=-3x²+24x(3≤x<8).
(2)S=-3x²+24x=-3(x-4)²+48.
∵3≤x<8,
∴当x=4时,S有最大值,最大值为48.
答:当AB的长为4米时,花圃的面积最大,最大值是48平方米.
2. 某商品的进价为每件 40 元,当售价为每件 60 元时,每个月可售出 100 件. 根据市场行情,现决定涨价销售,调查反映,每件商品的售价每涨价 1 元,每月要少卖出 2 件. 设每件商品的售价为 x(x 为整数)元,每个月的销量为 y 件.
(1)求 y 与 x 之间的函数关系式,并写出 x 的取值范围;
(2)当每件商品的售价定为多少元时,月销售利润最大? 最大月销售利润为多少元?
(1)求 y 与 x 之间的函数关系式,并写出 x 的取值范围;
(2)当每件商品的售价定为多少元时,月销售利润最大? 最大月销售利润为多少元?
答案:
2.解:
(1)由题意得y=100-2(x-60)=220-2x.
∵x-60≥0且220-2x≥0,
∴x的取值范围为60≤x≤110,且x为整数.
答:y与x之间的函数关系式为y=220-2x(60≤x≤110,且x为整数).
(2)设月销售利润为w元,则w=(220-2x)(x-40)=-2x²+300x-8800=-2(x-75)²+2450,
∵60≤x≤110,
∴当x=75时,w取得最大值,最大值为2450.
答:当每件商品的售价定为75元时,月销售利润最大,最大月销售利润为2450元.
(1)由题意得y=100-2(x-60)=220-2x.
∵x-60≥0且220-2x≥0,
∴x的取值范围为60≤x≤110,且x为整数.
答:y与x之间的函数关系式为y=220-2x(60≤x≤110,且x为整数).
(2)设月销售利润为w元,则w=(220-2x)(x-40)=-2x²+300x-8800=-2(x-75)²+2450,
∵60≤x≤110,
∴当x=75时,w取得最大值,最大值为2450.
答:当每件商品的售价定为75元时,月销售利润最大,最大月销售利润为2450元.
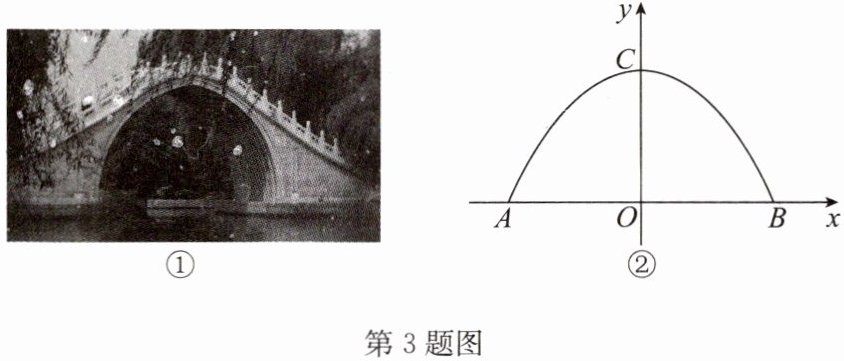
3. 如图①,单孔拱桥的形状近似于抛物线,建立如图②所示的平面直角坐标系,在正常水位时,水面宽度 AB 为 12 m,拱桥的最高点 C 到水面 AB 的距离为 6 m.
(1)求抛物线的函数解析式;
(2)因为上游水库泄洪,水面宽度变为 10 m,求水面上涨的高度.
(1)求抛物线的函数解析式;
(2)因为上游水库泄洪,水面宽度变为 10 m,求水面上涨的高度.

答案:
3.解:
(1)设抛物线的函数解析式为y=ax²+k,
由题意,得B(6,0),C(0,6),
将B(6,0),C(0,6)代入y=ax²+k,
得{k=6,
36a+k=0,
解得{k=6,
a=-1/6.
∴抛物线的函数解析式为y=-1/6x²+6.
(2)由题意得,水面上涨后,水面与抛物线的交点的横坐标为-5和5.
令x=5,则y=-1/6×5²+6=-25/6+6=11/6.
答:水面上涨的高度为11/6m.
(1)设抛物线的函数解析式为y=ax²+k,
由题意,得B(6,0),C(0,6),
将B(6,0),C(0,6)代入y=ax²+k,
得{k=6,
36a+k=0,
解得{k=6,
a=-1/6.
∴抛物线的函数解析式为y=-1/6x²+6.
(2)由题意得,水面上涨后,水面与抛物线的交点的横坐标为-5和5.
令x=5,则y=-1/6×5²+6=-25/6+6=11/6.
答:水面上涨的高度为11/6m.
查看更多完整答案,请扫码查看


