1. 求直线$y = 2x + 8与抛物线y = x^{2}的交点A$,$B$的坐标(点$A在点B$的左侧)及$\triangle AOB$的面积.
答案:
解:联立两个函数解析式可得{y=x²,
y=2x+8,
解得{x₁=-2,y₁=4,{x₂=4,y₂=16,
∴A(-2,4),B(4,16).
∴△AOB的面积=(2+4)×16-1/2×2×4-1/2×4×16-1/2×(2+4)×(16-4)=24.
y=2x+8,
解得{x₁=-2,y₁=4,{x₂=4,y₂=16,
∴A(-2,4),B(4,16).
∴△AOB的面积=(2+4)×16-1/2×2×4-1/2×4×16-1/2×(2+4)×(16-4)=24.
2. 如图,在平面直角坐标系中,$O$为坐标原点,抛物线$y = -\frac{1}{2}x^{2} + bx与x轴正半轴交于点A$,点$B是y$轴负半轴上一点,点$A关于点B的对称点C$在该抛物线上,过点$C作y轴的垂线交抛物线于点D$,连接$OC$,$AD$. 若点$C的横坐标为-2$,求四边形$OCDA$的面积.
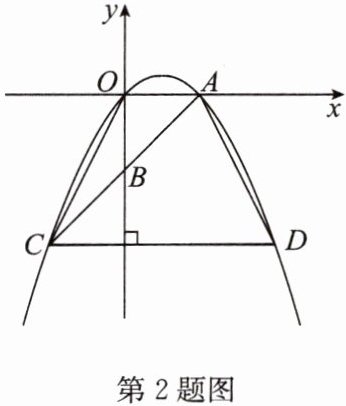

答案:
解:
∵点A与点C关于点B对称,而点C的横坐标为-2,
∴A(2,0),把A(2,0)代入y=-1/2x²+bx,
得-2+2b=0,解得b=1,
∴抛物线的函数解析式为y=-1/2x²+x.
当x=-2时,y=-1/2x²+x=-2-2=-4,
∴C(-2,-4).
∵抛物线的对称轴为直线x=-1/(2×(-1/2))=1,
∴D(4,-4),
∴CD=4-(-2)=6,
∴四边形OCDA的面积=1/2×(2+6)×4=16.
∵点A与点C关于点B对称,而点C的横坐标为-2,
∴A(2,0),把A(2,0)代入y=-1/2x²+bx,
得-2+2b=0,解得b=1,
∴抛物线的函数解析式为y=-1/2x²+x.
当x=-2时,y=-1/2x²+x=-2-2=-4,
∴C(-2,-4).
∵抛物线的对称轴为直线x=-1/(2×(-1/2))=1,
∴D(4,-4),
∴CD=4-(-2)=6,
∴四边形OCDA的面积=1/2×(2+6)×4=16.
查看更多完整答案,请扫码查看


