《2025年阳光同学课时优化作业五年级数学上册北师大版广东专版》

1. 把 3 和 5 的倍数(40 以内)写在下面圈中合适的位置,并填空。

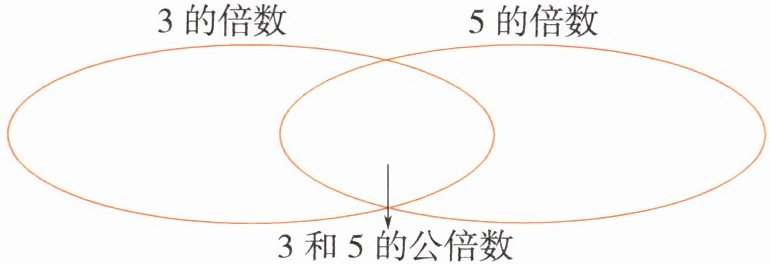
40 以内 3 和 5 的公倍数有( ),其中最小公倍数是( )。

答案：
15,30　15

2.(迁移探究)在括号里写出下面各组数的最小公倍数。
2 和 5(10) 6 和 7(42) 7 和 11(77) 5 和 8(40)
18 和 1(18) 9 和 72(72) 13 和 65(65) 78 和 39(78)
我发现:当两个数的公因数只有(1)时,这两个数的最小公倍数是(两个数的积)。当两个数中较大数是较小数的(倍数)时,这两个数的最小公倍数是(较大数)。

答案： 10　42　77　40　　18　72　65　78 1　两个数的积 倍数　较大数

3. 求下面各组数的最小公倍数。
10 和 40 18 和 27 25 和 12 72 和 48

答案： 40　54　300　144

4. 填空。
(1)若$A= 2×2×3$,$B= 2×3×5$,则 A 和 B 的最大公因数是(6),A 和 B 的最小公倍数是(60)。
(2)(泉州真题)五(3)班同学用长 18 cm、宽 12 cm 的长方形纸板剪、拼正方形。明明从这样的纸板上剪出若干个一样的小正方形,刚好剪完,没有剩余,正方形的边长最长是(6)cm;花花用若干张这样的长方形纸板拼一个大正方形,至少需要(6)张。

答案：
(1)6　60　
(2)6　6

5.(衢州真题)丁丁的妈妈在体育馆的跑道上跑一圈需要 4 分,爸爸跑一圈需要 3 分,丁丁跑一圈需要 6 分。妈妈和丁丁同时从起点出发,几分后可以在起点第一次相遇? (写出你的思考过程)

答案： 2⟌4 6
2 3
2×2×3=12,4和6的最小公倍数是12，所以12分后妈妈和丁丁可以在起点第一次相遇

6.(丽水真题)某校五年级参加植树的学生人数在 20~50 之间,如果每 2 人一组、每 6 人一组或每 9 人一组,都多 1 人。该校五年级有多少人参加植树活动?

答案： 2,6和9的最小公倍数是18，又因为学生人数在20~50人之间，所以五年级参加植树的学生人数有:18×2+1=37(人)