(1)等式的左右两边同时加上或减去
同一个
数,等式仍然成立。根据这种性质可以解简单的方程。
答案:
同一个
(2)使方程左右两边
相等
的未知数
的值,叫作方程的解。
答案:
相等 未知数
(1)$x + 25 = 60$
解:$x + 25$
$x =$
(2)$x - 15 = 40$
解:$x - 15$
$x =$
解:$x + 25$
-
25
$= 60$-
25
$x =$
35
(2)$x - 15 = 40$
解:$x - 15$
+
15
$= 40$+
15
$x =$
55
答案:
(1)- 25 - 25 35
(2)+ 15 + 15 55
(1)- 25 - 25 35
(2)+ 15 + 15 55
3. 解方程并检验。
$x + 2.7 = 6.5$ $0.6 + x = 3.8$
$x - 37 = 86$ $x - 3.8 = 4.2$
$x + 2.7 = 6.5$ $0.6 + x = 3.8$
$x - 37 = 86$ $x - 3.8 = 4.2$
答案:
方程$x + 2.7 = 6.5$
解:
$x+2.7 - 2.7=6.5 - 2.7$
$x = 3.8$
检验:
把$x = 3.8$代入方程左边$=3.8 + 2.7=6.5$,方程右边$=6.5$,左边$=$右边,所以$x = 3.8$是方程的解。
方程$0.6 + x = 3.8$
解:
$0.6+x - 0.6=3.8 - 0.6$
$x = 3.2$
检验:
把$x = 3.2$代入方程左边$=0.6 + 3.2=3.8$,方程右边$=3.8$,左边$=$右边,所以$x = 3.2$是方程的解。
方程$x - 37 = 86$
解:
$x-37 + 37=86 + 37$
$x = 123$
检验:
把$x = 123$代入方程左边$=123 - 37=86$,方程右边$=86$,左边$=$右边,所以$x = 123$是方程的解。
方程$x - 3.8 = 4.2$
解:
$x-3.8 + 3.8=4.2 + 3.8$
$x = 8$
检验:
把$x = 8$代入方程左边$=8 - 3.8=4.2$,方程右边$=4.2$,左边$=$右边,所以$x = 8$是方程的解。
综上,方程$x + 2.7 = 6.5$的解为$x = 3.8$;方程$0.6 + x = 3.8$的解为$x = 3.2$;方程$x - 37 = 86$的解为$x = 123$;方程$x - 3.8 = 4.2$的解为$x = 8$。
解:
$x+2.7 - 2.7=6.5 - 2.7$
$x = 3.8$
检验:
把$x = 3.8$代入方程左边$=3.8 + 2.7=6.5$,方程右边$=6.5$,左边$=$右边,所以$x = 3.8$是方程的解。
方程$0.6 + x = 3.8$
解:
$0.6+x - 0.6=3.8 - 0.6$
$x = 3.2$
检验:
把$x = 3.2$代入方程左边$=0.6 + 3.2=3.8$,方程右边$=3.8$,左边$=$右边,所以$x = 3.2$是方程的解。
方程$x - 37 = 86$
解:
$x-37 + 37=86 + 37$
$x = 123$
检验:
把$x = 123$代入方程左边$=123 - 37=86$,方程右边$=86$,左边$=$右边,所以$x = 123$是方程的解。
方程$x - 3.8 = 4.2$
解:
$x-3.8 + 3.8=4.2 + 3.8$
$x = 8$
检验:
把$x = 8$代入方程左边$=8 - 3.8=4.2$,方程右边$=4.2$,左边$=$右边,所以$x = 8$是方程的解。
综上,方程$x + 2.7 = 6.5$的解为$x = 3.8$;方程$0.6 + x = 3.8$的解为$x = 3.2$;方程$x - 37 = 86$的解为$x = 123$;方程$x - 3.8 = 4.2$的解为$x = 8$。
4. 根据图中的数量关系列方程并解答。
(1)

钢笔比文具盒便宜 7.6 元。
(2)
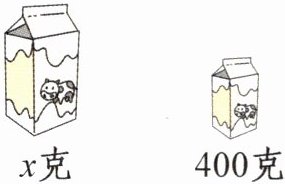
大盒净含量比小盒多 250 克。
(3)
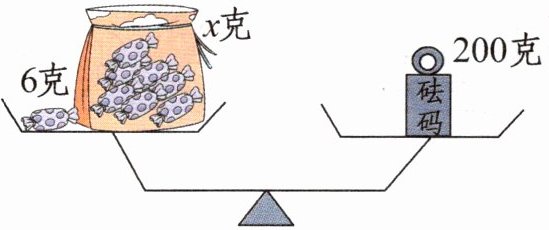
(1)

钢笔比文具盒便宜 7.6 元。
(2)

大盒净含量比小盒多 250 克。
(3)

答案:
(1)x-13.6=7.6 x=21.2
(2)x-400=250 x=650
(3)x+6=200 x=194
(1)x-13.6=7.6 x=21.2
(2)x-400=250 x=650
(3)x+6=200 x=194
5. 素养题 根据下面图形中数的排列规律,用含有字母$A的式子表示B$,并求出$A$、$B$的值。
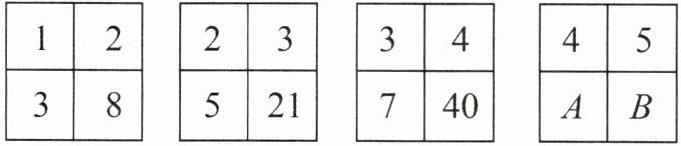

答案:
B=(4+A)×5=5(4+A) A=4+5=9 B=5×(4+9)=65
查看更多完整答案,请扫码查看


