1. 下面的图形各有几条对称轴?

(

(

(
5
)条 (5
)条
(
3
)条 (2
)条
答案:
5 5 3 2
2. 先画出下面每个图形的对称轴,再完成填空。

①有(

①有(
4
)条对称轴,②有(3
)条对称轴,③有(无数
)条对称轴。
答案:
1. 首先分析图形①:
图形①是一个正方形内有一个内切圆,正方形的对称轴就是这个组合图形的对称轴。
正方形对称轴的数量:
正方形有$4$条对称轴,分别是两条对角线所在直线和两组对边中点连线所在直线。
2. 然后分析图形②:
图形②是一个等边三角形内有一个内切椭圆,等边三角形的对称轴就是这个组合图形的对称轴。
等边三角形对称轴的数量:
等边三角形有$3$条对称轴,分别是三条高(或角平分线、中线)所在直线。
3. 最后分析图形③:
图形③是一个圆内有一个内接正方形,圆的对称轴就是这个组合图形的对称轴。
圆对称轴的数量:
圆有无数条对称轴,因为过圆心的任意一条直线都是圆的对称轴。
所以①有$4$条对称轴,②有$3$条对称轴,③有无数条对称轴。
图形①是一个正方形内有一个内切圆,正方形的对称轴就是这个组合图形的对称轴。
正方形对称轴的数量:
正方形有$4$条对称轴,分别是两条对角线所在直线和两组对边中点连线所在直线。
2. 然后分析图形②:
图形②是一个等边三角形内有一个内切椭圆,等边三角形的对称轴就是这个组合图形的对称轴。
等边三角形对称轴的数量:
等边三角形有$3$条对称轴,分别是三条高(或角平分线、中线)所在直线。
3. 最后分析图形③:
图形③是一个圆内有一个内接正方形,圆的对称轴就是这个组合图形的对称轴。
圆对称轴的数量:
圆有无数条对称轴,因为过圆心的任意一条直线都是圆的对称轴。
所以①有$4$条对称轴,②有$3$条对称轴,③有无数条对称轴。
3. 素养题 下面哪些数字或汉字是轴对称图形?请圈出来。


答案:


4. 在方格纸上设计一个有2条对称轴的图形,并画出它的对称轴。


答案:

5. 把一张正方形纸片如图①、图②对折两次后,再如图③挖去一个三角形小孔,则展开后图形是(

C
)。
答案:
C
6. 想一想,如何把“p”变成“q”。


答案:
本题可根据轴对称图形的性质,通过轴对称变换把“p”变成“q”。
步骤如下:
1. 确定对称轴:观察“p”和“q”的形状,可发现以“p”右侧的竖线为对称轴进行轴对称变换能得到“q”。
2. 实施变换:以“p”右侧的竖线为对称轴,将“p”沿此对称轴对折,使“p”左右两侧完全重合,此时“p”就变成了“q”。
综上,把“p”沿其右侧的竖线进行轴对称变换可变成“q”。
步骤如下:
1. 确定对称轴:观察“p”和“q”的形状,可发现以“p”右侧的竖线为对称轴进行轴对称变换能得到“q”。
2. 实施变换:以“p”右侧的竖线为对称轴,将“p”沿此对称轴对折,使“p”左右两侧完全重合,此时“p”就变成了“q”。
综上,把“p”沿其右侧的竖线进行轴对称变换可变成“q”。
7. 如图,一个等边三角形被分成了若干个同样的小等边三角形。有些小三角形已被涂蓝,那么最少再涂蓝几个小三角形就可以构成轴对称图形?


答案:
3 个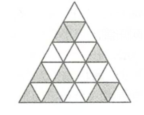
3 个

查看更多完整答案,请扫码查看


