《2025年一遍过八年级物理上册沪科版》

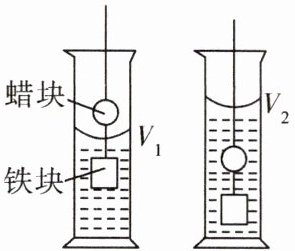
1 实验室里常用沉坠法测蜡块的密度。如图所示,量筒内原来水的体积为$V_{0}$,只浸没铁块时,量筒内水与铁块的总体积为$V_{1}$,将蜡块及铁块全浸入水中后,量筒内水、铁块和蜡块的总体积为$V_{2}$。已知蜡块的质量为$m$,则蜡块的密度为(B)

A.$\dfrac{m}{V_{0}}$

B.$\dfrac{m}{V_{2}-V_{1}}$
C.$\dfrac{m}{V_{2}+V_{1}}$
D.$\dfrac{m}{V_{2}-V_{1}-V_{0}}$

答案： 解：蜡块的体积为铁块和蜡块的总体积减去铁块的体积，即$V = V_{2} - V_{1}$。
蜡块的密度公式为$\rho = \frac{m}{V}$，将$V = V_{2} - V_{1}$代入，可得$\rho = \frac{m}{V_{2} - V_{1}}$。
答案：B

(1)拆下穿过“花生”的细绳,用天平测“花生”质量,操作正确,如图所示,“花生”的质量为2.8g。
(2)因“花生”体积较小,选择分度值更小的注射器来测“花生”体积。其步骤如图,步骤②中摇动注射器的目的是使“花生”完全浸没在水中。
(3)测得“花生”的密度为2.8$g/cm^{3}$。若在步骤③中,不慎挤出少许水,则密度测量值偏大。

答案：
(1)2.8
(2)使“花生”完全浸没在水中
(3)2.8；大

3 小明利用如下器材测量鸡蛋的密度:托盘天平、溢水杯、烧杯、量筒、鸡蛋、足量的水。实验步骤如下:

(1)把鸡蛋放入调节好的天平左盘,在右盘内增减砝码,并调节游码,天平平衡后,右盘中所放砝码的质量及游码在标尺上的位置如图甲所示,则该鸡蛋的质量为58.0g。
(2)由于鸡蛋较大,不能用量筒直接测量其体积,而要利用溢水杯来测量。将适量的水倒入溢水杯中,让水面与溢水口相平,再将鸡蛋轻轻放入溢水杯中,浸没在水中后,鸡蛋所排开的水全部盛于烧杯中,如图乙所示。
(3)将烧杯中的水倒入量筒,如图丙所示,则溢出水的体积为50mL。
(4)通过计算可得鸡蛋的密度为1.16×10³$kg/m^{3}$。
(5)实验过程中,误差不可避免,针对本实验请写出一个产生误差的可能原因:烧杯中的水倒入量筒时倒不干净，导致测量的溢出水的体积偏小。

答案：
(1)58.0
(3)50
(4)1.16×10³
(5)烧杯中的水倒入量筒时倒不干净，导致测量的溢出水的体积偏小

(1)请按照图甲的顺序将相应的实验步骤补充完整。
第一步:测出空瓶的质量$m_{1}$;
第二步:用天平测出小瓶装满水的总质量$m_2$;
第三步:瓶装满酱油时,测得酱油和瓶的总质量如图乙中砝码和游码所示,其结果$m_{3}=$47.4g。
(2)请根据小明的实验步骤及数据帮他写出酱油密度的表达式:$\rho_{酱油}=$$\frac{m_{3}-m_{1}}{m_{2}-m_{1}}\rho_{水}$(用字母表示)。小明第三次测量时,酱油未完全装满,由此测出的密度将偏小(填“大”或“小”)。

答案： 【解析】：
本题考查密度的测量。
需要测酱油的密度，没有量筒，但有天平和小空瓶，可通过测出空瓶的质量，装满水后测出总质量，从而得出水的质量，根据公式$V=\frac{m}{\rho}$，求出水的体积，即瓶子的容积，装满酱油后测出酱油和瓶子的总质量，从而得出酱油的质量，酱油的体积等于瓶子的容积，再根据公式$\rho=\frac{m}{V}$求出酱油的密度；若酱油未完全装满，则测出的酱油的质量偏小，根据公式$\rho=\frac{m}{V}$，求出的密度偏小。
实验步骤为：
第一步：测出空瓶的质量$m_1$。
第二步：用天平测出小瓶装满水的总质量$m_2$。
第三步：瓶装满酱油时，测得酱油和瓶的总质量如图乙中砝码和游码所示，其结果$m_3=47.4g$。
酱油密度的表达式为：
$\rho_{酱油}=\frac{m_{酱油}}{V_{酱油}}=\frac{m_{3}-m_{1}}{\frac{m_{2}-m_{1}}{\rho_{水}}}=\frac{m_{3}-m_{1}}{m_{2}-m_{1}}\rho_{水}$，
第三次测量时，酱油未完全装满，会导致测得的酱油的质量偏小，根据公式$\rho=\frac{m}{V}$，测出的密度将偏小。
【答案】：
(1)用天平测出小瓶装满水的总质量$m_2$；$47.4$。
(2)$\frac{m_{3}-m_{1}}{m_{2}-m_{1}}\rho_{水}$；小。