第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1 [2025贵阳月考]直角三角形中两直角边长分别为a,b,斜边长为c,则勾股定理的表示为(
A. $a^{2}+b^{2}= c^{2}$
B. $b^{2}+c^{2}= a^{2}$
C. $a^{2}+c^{2}= b^{2}$
D. $a^{2}-c^{2}= b^{2}$
A
)A. $a^{2}+b^{2}= c^{2}$
B. $b^{2}+c^{2}= a^{2}$
C. $a^{2}+c^{2}= b^{2}$
D. $a^{2}-c^{2}= b^{2}$
答案:
A
易错提醒
运用勾股定理应注意的问题
(1)勾股定理使用的前提是在直角三角形中;
(2)要分清斜边和直角边,在Rt△ABC中,∠C不一定是直角。
易错提醒
运用勾股定理应注意的问题
(1)勾股定理使用的前提是在直角三角形中;
(2)要分清斜边和直角边,在Rt△ABC中,∠C不一定是直角。
2 你听说过亡羊补牢的故事吧!为了防止羊的再次丢失,牧羊人要在如图所示的宽9dm、长12dm的长方形栅栏门的相对角的顶点钉一根加固木条,则这根木条的长至少为(

)
A. 9dm
B. 12dm
C. 15dm
D. 21dm

)
A. 9dm
B. 12dm
C. 15dm
D. 21dm
答案:
C 如图,在Rt△ABC中,∠ABC=90°,所以AB²+BC²=AC²,即12²+9²=AC²,所以AC=15dm。

C 如图,在Rt△ABC中,∠ABC=90°,所以AB²+BC²=AC²,即12²+9²=AC²,所以AC=15dm。

3 [2025杭州拱墅区期末]一个直角三角形,若三边的平方和为200,则斜边长为(
A. 8
B. 9
C. 10
D. 11
10
)A. 8
B. 9
C. 10
D. 11
答案:
C 设直角三角形的三边长为a,b,c,其中c为斜边,则a²+b²=c²。因为这个直角三角形的三边长的平方和为200,所以a²+b²+c²=200,所以2c²=200,所以c²=100,所以c=10,即斜边长为10。
4 [2025黔东南州质检]底边长为16cm,底边上的高为6cm的等腰三角形的腰长为( )
A. 8cm
B. 9cm
C. 10cm
D. 12cm
A. 8cm
B. 9cm
C. 10cm
D. 12cm
答案:
C 如图,由题意,得AB=AC,BC=16cm,AD⊥BC,AD=6cm,所以BD=8cm(等腰三角形的“三线合一”),由勾股定理,得AB²=AD²+BD²,所以AB=AC=10cm。

C 如图,由题意,得AB=AC,BC=16cm,AD⊥BC,AD=6cm,所以BD=8cm(等腰三角形的“三线合一”),由勾股定理,得AB²=AD²+BD²,所以AB=AC=10cm。

5 [2024咸阳秦都区期末]已知某直角三角形的两条直角边长的比为5:12,若该直角三角形的周长为60,则该直角三角形的斜边长为____
[变式][2024泰州二附中期末]在$Rt\triangle ABC$中,$∠C= 90^{\circ },AB-BC= 1,AC= 4$,则$BC= $____
26
。[变式][2024泰州二附中期末]在$Rt\triangle ABC$中,$∠C= 90^{\circ },AB-BC= 1,AC= 4$,则$BC= $____
7.5
。
答案:
26 设直角三角形的两条直角边长分别为5x(x>0),12x,因为(5x)²+(12x)²=(13x)²,所以斜边长为13x,又因为直角三角形的周长为60,所以5x+12x+13x=60,解得x=2,所以斜边长为13×2=26。
变式 7.5 设BC=x,则AB=BC+1=x+1,在Rt△ABC中,∠C=90°,由勾股定理可知AC²+BC²=AB²,即4²+x²=(x+1)²,所以x=7.5,即BC=7.5。
变式 7.5 设BC=x,则AB=BC+1=x+1,在Rt△ABC中,∠C=90°,由勾股定理可知AC²+BC²=AB²,即4²+x²=(x+1)²,所以x=7.5,即BC=7.5。
6 [2025泰州期中]如图,在$\triangle ABC$中,$∠BAC= 90^{\circ },AB= 3,AC= 4,AD⊥BC$,垂足为D。
求:(1)BC的长为
(2)AD的长为
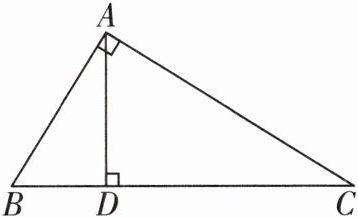
求:(1)BC的长为
5
;(2)AD的长为
$\frac{12}{5}$
。
答案:
解:
(1)在Rt△ABC中,∠BAC=90°,AB=3,AC=4,所以BC²=AB²+AC²=3²+4²=25,所以BC=5。
(2)因为AD⊥BC于点D,所以$S_{△ABC}= \frac{1}{2}AB·AC= \frac{1}{2}BC·AD($等积法),所以$\frac{1}{2}×3×4= \frac{1}{2}×5×AD,$所以$AD= \frac{12}{5}。$
[注]波浪线标注部分为解题关键,助你快速解题。
(1)在Rt△ABC中,∠BAC=90°,AB=3,AC=4,所以BC²=AB²+AC²=3²+4²=25,所以BC=5。
(2)因为AD⊥BC于点D,所以$S_{△ABC}= \frac{1}{2}AB·AC= \frac{1}{2}BC·AD($等积法),所以$\frac{1}{2}×3×4= \frac{1}{2}×5×AD,$所以$AD= \frac{12}{5}。$
[注]波浪线标注部分为解题关键,助你快速解题。
7 [教材随堂练习变式][2025大庆四校月考]如图,阴影部分是两个正方形,其他三个图形是一个正方形和两个直角三角形,则阴影部分的面积之和为____。
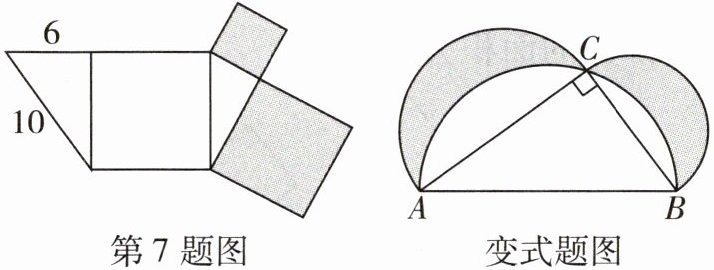
[变式][2024张掖甘州区三模]如图,在$\triangle ABC$中,$∠ACB= 90^{\circ }$,分别以三边为直径向上作三个半圆。若$AB= 5,AC= 4$,则阴影部分图形的面积为____。

[变式][2024张掖甘州区三模]如图,在$\triangle ABC$中,$∠ACB= 90^{\circ }$,分别以三边为直径向上作三个半圆。若$AB= 5,AC= 4$,则阴影部分图形的面积为____。
答案:
64 如图,因为四边形ABCD是正方形,所以AB=CD,在Rt△CDE中,由勾股定理,得CD²=CE²-DE²=10²-6²=64,在Rt△ABF中,由勾股定理,得AB²=AF²+BF²,所以阴影部分的面积之和为AF²+BF²=AB²=CD²=64。

变式 6 因为∠ACB=90°,AB=5,AC=4,所以BC²=AB²-AC²=9,所以BC=3,$S_{△ABC}= \frac{1}{2}BC·AC= \frac{1}{2}×3×4=6,$设以BC为直径的半圆的面积为S₁,以AC为直径的半圆的面积为S₂,以AB为直径的半圆的面积为S₃,因为$S₁= \frac{1}{2}π·(\frac{1}{2}BC)²= \frac{π}{8}BC²,$$S₂= \frac{1}{2}π·(\frac{1}{2}AC)²= \frac{π}{8}AC²,$$S₃= \frac{1}{2}π·(\frac{1}{2}AB)²= \frac{π}{8}AB²,$所以$S_{阴影}=S₁+S₂+S_{△ABC}-S₃= \frac{π}{8}(BC²+AC²-AB²)+S_{△ABC}=S_{△ABC}=6。$
64 如图,因为四边形ABCD是正方形,所以AB=CD,在Rt△CDE中,由勾股定理,得CD²=CE²-DE²=10²-6²=64,在Rt△ABF中,由勾股定理,得AB²=AF²+BF²,所以阴影部分的面积之和为AF²+BF²=AB²=CD²=64。

变式 6 因为∠ACB=90°,AB=5,AC=4,所以BC²=AB²-AC²=9,所以BC=3,$S_{△ABC}= \frac{1}{2}BC·AC= \frac{1}{2}×3×4=6,$设以BC为直径的半圆的面积为S₁,以AC为直径的半圆的面积为S₂,以AB为直径的半圆的面积为S₃,因为$S₁= \frac{1}{2}π·(\frac{1}{2}BC)²= \frac{π}{8}BC²,$$S₂= \frac{1}{2}π·(\frac{1}{2}AC)²= \frac{π}{8}AC²,$$S₃= \frac{1}{2}π·(\frac{1}{2}AB)²= \frac{π}{8}AB²,$所以$S_{阴影}=S₁+S₂+S_{△ABC}-S₃= \frac{π}{8}(BC²+AC²-AB²)+S_{△ABC}=S_{△ABC}=6。$
查看更多完整答案,请扫码查看


