第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
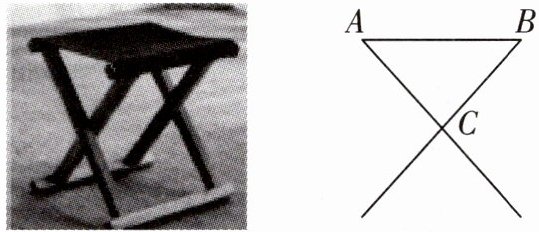
1 如图是某款折叠凳及其侧面示意图,若$AC= BC= 18cm$,则此折叠凳的宽AB可能为(
A.70 cm
B.55 cm
C.40 cm
D.25 cm
D
)
A.70 cm
B.55 cm
C.40 cm
D.25 cm
答案:
D
∵AC=BC=18cm,
∴0cm<AB<36cm,
∴此折叠凳的宽AB可能为25cm.
∵AC=BC=18cm,
∴0cm<AB<36cm,
∴此折叠凳的宽AB可能为25cm.
2 教材练习变式[2025衡水模拟]将周长为12 cm的三角形的三条边依次放在一条直线上,其中所标数据正确的是(
D
)
答案:
D
∵4+2=6,不符合组成三角形的条件,
∴A选项中所标的数据不正确;
∵3+3=6,不符合组成三角形的条件,
∴B选项中所标的数据不正确;
∵3+2<7,不符合组成三角形的条件,
∴C选项中所标的数据不正确;
∵5+2>5,符合组成三角形的条件,
∴D选项中所标的数据正确.
∵4+2=6,不符合组成三角形的条件,
∴A选项中所标的数据不正确;
∵3+3=6,不符合组成三角形的条件,
∴B选项中所标的数据不正确;
∵3+2<7,不符合组成三角形的条件,
∴C选项中所标的数据不正确;
∵5+2>5,符合组成三角形的条件,
∴D选项中所标的数据正确.
3 [2025大理州期末]已知$\triangle ABC$的三边长分别为6,5,x,则x的取值范围是
1<x<11
.
答案:
1<x<11 根据三角形的三边关系,得6 - 5<x<6 + 5,即1<x<11.
(1)a,b,c只需要满足条件
(2)若$a= 2,c= 5$,b为整数,求组成的三角形的周长.
解:由题意,得{c - a < b < c + a,a < b < c,即{5 - 2 < b < 5 + 2,2 < b < 5,解得3 < b < 5.
∵b为整数,
∴b = 4,
∴组成的三角形的周长为a + b + c = 2 + 4 + 5 = 11.
①
即可.(只填一个序号)(2)若$a= 2,c= 5$,b为整数,求组成的三角形的周长.
解:由题意,得{c - a < b < c + a,a < b < c,即{5 - 2 < b < 5 + 2,2 < b < 5,解得3 < b < 5.
∵b为整数,
∴b = 4,
∴组成的三角形的周长为a + b + c = 2 + 4 + 5 = 11.
答案:
解:
(1)①
(2)由题意,得{c - a < b < c + a,a < b < c,即{5 - 2 < b < 5 + 2,2 < b < 5,解得3 < b < 5.
∵b为整数,
∴b = 4,
∴组成的三角形的周长为a + b + c = 2 + 4 + 5 = 11.
(1)①
(2)由题意,得{c - a < b < c + a,a < b < c,即{5 - 2 < b < 5 + 2,2 < b < 5,解得3 < b < 5.
∵b为整数,
∴b = 4,
∴组成的三角形的周长为a + b + c = 2 + 4 + 5 = 11.
5 [2025扬州江都区八校联考]已知$\triangle ABC$的三边长均为整数,$\triangle ABC$的周长为偶数.
(1)若$AC= 9,BC= 3$,求AB的长度;
(2)若$AC+BC= 15$,求AB长度的最大值.
(1)若$AC= 9,BC= 3$,求AB的长度;
(2)若$AC+BC= 15$,求AB长度的最大值.
答案:
解:
(1)根据三角形的三边关系,得AC - BC<AB<AC + BC,即9 - 3<AB<9 + 3,解得6<AB<12.
∵△ABC的周长为偶数,而AC,BC的长度为奇数,
∴AB的长度为偶数,且为正整数.
∴AB = 8或10,即AB的长度为8或10.
(2)
∵AC + BC = 15,△ABC的周长为偶数,
∴AB的长度为奇数,且为正整数.又
∵AB<AC + BC = 15,
∴AB长度的最大值为13.
(1)根据三角形的三边关系,得AC - BC<AB<AC + BC,即9 - 3<AB<9 + 3,解得6<AB<12.
∵△ABC的周长为偶数,而AC,BC的长度为奇数,
∴AB的长度为偶数,且为正整数.
∴AB = 8或10,即AB的长度为8或10.
(2)
∵AC + BC = 15,△ABC的周长为偶数,
∴AB的长度为奇数,且为正整数.又
∵AB<AC + BC = 15,
∴AB长度的最大值为13.
6 在$\triangle ABC$中,$AB>AC$,比较大小:$∠C$
>
$∠B$.
答案:
>
7 在$\triangle ABC$中,$AC= 3,BC= 5$,且$∠C>∠A>∠B$,则AB的长度的取值范围为
5<AB<8
.
答案:
5<AB<8
∵AC = 3,BC = 5,
∴2<AB<8.
∵∠C>∠A>∠B,
∴AB>BC>AC,
∴AB>5>3,
∴5<AB<8.
∵AC = 3,BC = 5,
∴2<AB<8.
∵∠C>∠A>∠B,
∴AB>BC>AC,
∴AB>5>3,
∴5<AB<8.
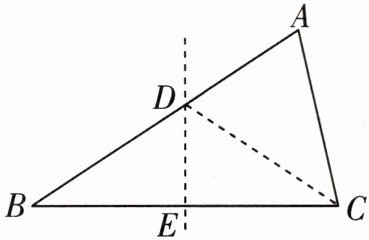
8 天星原创教材通过折纸的方式证明了“大边对大角”.“飞翔”数学兴趣小组的学生发现“大角对大边”也可利用线段的对称轴进行类似的证明.如图,在$\triangle ABC$中,$∠ACB>∠B$,为了证明$AB>AC$,作BC的垂直平分线,交AB于点D,交BC于点E,连接DC.请你帮助“飞翔”数学兴趣小组的学生完成证明过程.

答案:
解:
∵垂直平分线DE是线段BC的对称轴,
∴BD = CD.在△ACD中,AD + CD>AC,
∴AD + BD>AC,
∴AB>AC.
∵垂直平分线DE是线段BC的对称轴,
∴BD = CD.在△ACD中,AD + CD>AC,
∴AD + BD>AC,
∴AB>AC.
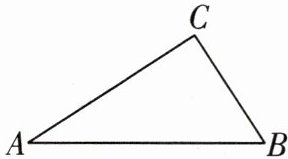
9 教材问题变式如图,在$\triangle ABC$中,已知$AB>AC>BC$.求证:$∠C>∠B>∠A$.

答案:
证明:如图1,将△ABC折叠,使边AC落在边AB上,点C落在边AB上的点C'处,折痕AD交BC于点D,则∠AC'D = ∠C.
∵∠AC'D = ∠B + ∠BDC',
∴∠AC'D>∠B,
∴∠C>∠B.
如图2,将△ABC折叠,使边CB落在边CA上,点B落在边CA上的点B'处,折痕CE交AB于点E,则∠CB'E = ∠B.
∵∠CB'E = ∠A + ∠AEB',
∴∠CB'E>∠A,
∴∠B>∠A.
∴∠C>∠B>∠A.
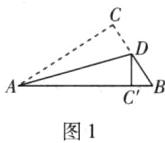

证明:如图1,将△ABC折叠,使边AC落在边AB上,点C落在边AB上的点C'处,折痕AD交BC于点D,则∠AC'D = ∠C.
∵∠AC'D = ∠B + ∠BDC',
∴∠AC'D>∠B,
∴∠C>∠B.
如图2,将△ABC折叠,使边CB落在边CA上,点B落在边CA上的点B'处,折痕CE交AB于点E,则∠CB'E = ∠B.
∵∠CB'E = ∠A + ∠AEB',
∴∠CB'E>∠A,
∴∠B>∠A.
∴∠C>∠B>∠A.


查看更多完整答案,请扫码查看


