《2025年暑假生活北京师范大学出版社四年级数学海南专版》

五、下面是三个商店同一品牌、同一款式的三种商品的价格牌。

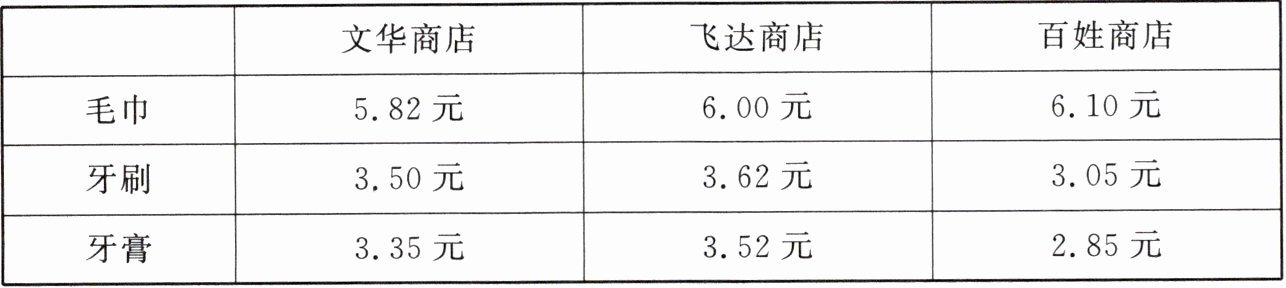
1. 哪个商店的毛巾最便宜？哪个商店的牙刷最贵？
文华商店的毛巾最便宜，飞达商店的牙刷最贵。
2. 如果买牙膏,应到哪个商店购买？为什么？
应到百姓商店购买牙膏，因为百姓商店的牙膏价格最低。

答案： 【解析】：
1. 比较毛巾价格：$5.82＜6.00＜6.10$，比较牙刷价格：$3.05＜3.50＜3.62$。
2. 比较牙膏价格：$2.85＜3.35＜3.52$。
【答案】：
1. 文华商店的毛巾最便宜，飞达商店的牙刷最贵。
2. 应到百姓商店购买牙膏，因为百姓商店的牙膏价格最低。

六、用最简便的方法计算。
1. $ 9999×7778+3333×6666 $ 2. $ 77×44+77×21+23×65 $

答案： 【解析】：
1. 对于$9999×7778 + 3333×6666$，先对$3333×6666$进行变形，$3333×6666=3333×3×2222 = 9999×2222$，则原式可转化为$9999×7778+9999×2222$，根据乘法分配律$a× c + b× c=(a + b)× c$，这里$a = 7778$，$b = 2222$，$c = 9999$，所以$9999×(7778 + 2222)=9999×10000 = 99990000$。
2. 对于$77×44+77×21+23×65$，先根据乘法分配律计算$77×44 + 77×21$，可得$77×(44 + 21)=77×65$，此时原式变为$77×65+23×65$，再根据乘法分配律，$a× c + b× c=(a + b)× c$，这里$a = 77$，$b = 23$，$c = 65$，所以$(77 + 23)×65=100×65 = 6500$。
【答案】：1. $99990000$；2. $6500$

快速算结果
1. $ 21+22+23+…+38+39 $ 2. $ 2488-(336+488+664) $

答案： 【解析】：
1. 对于$21 + 22 + 23+\cdots+38 + 39$，可利用等差数列求和公式$S_n=\frac{n(a_1 + a_n)}{2}$，其中$n$为项数，$a_1$为首项，$a_n$为末项。项数$n=39 - 21+1 = 19$，首项$a_1 = 21$，末项$a_n = 39$，则$S=\frac{19×(21 + 39)}{2}=19×30=570$。
2. 对于$2488-(336 + 488+664)$，根据去括号法则去掉括号得$2488 - 336 - 488 - 664$，然后利用加法交换律和结合律进行简便计算，即$(2488 - 488)-(336 + 664)=2000 - 1000 = 1000$。
【答案】：1. $570$；2. $1000$