1. 图甲是北京冬奥会中翻跃大跳台的情景。运动员不借助滑雪杖,只踩着雪板从高处滑行而下,通过起跳台起跳,完成各种空翻、转体等技术动作后落地。图乙中的虚线是比赛过程中运动员的轨迹。不计空气阻力,下列说法正确的是(
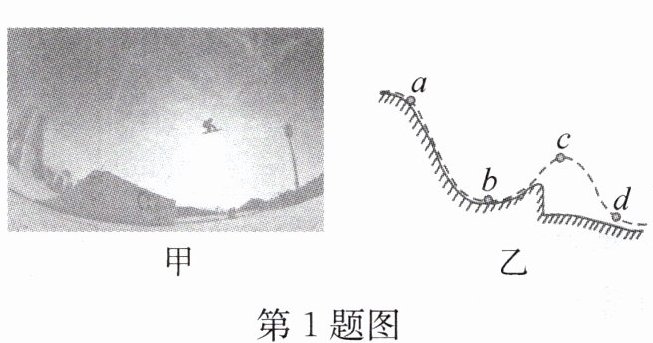
A.在a、b、c、d四点中,运动员在a点时的重力势能最大
B.从b点到c点的过程中,运动员的动能在增加
C.从c点到d点的过程中,运动员的机械能变小
D.a点和c点都是最高点,运动员分别在该两点时的动能都为零
A
)。
A.在a、b、c、d四点中,运动员在a点时的重力势能最大
B.从b点到c点的过程中,运动员的动能在增加
C.从c点到d点的过程中,运动员的机械能变小
D.a点和c点都是最高点,运动员分别在该两点时的动能都为零
答案:
A
2. 低空跳伞是一种极限运动。一名跳伞运动员背着伞包从某高层建筑顶层跳下,且一直沿竖直方向下落,整个运动过程的v-t图像如图所示,10s末时打开了降落伞。下列说法正确的是(

A.前10s内,运动员减少的重力势能全部转化为动能
B.10~15s,运动员和降落伞受到的空气阻力大于其总重力
C.15~30s,运动员和降落伞的动能增大
D.10~30s,运动员和降落伞的机械能总量保持不变
B
)。
A.前10s内,运动员减少的重力势能全部转化为动能
B.10~15s,运动员和降落伞受到的空气阻力大于其总重力
C.15~30s,运动员和降落伞的动能增大
D.10~30s,运动员和降落伞的机械能总量保持不变
答案:
B
3. 如图所示,一重2000N的物体被遗失在井中,现通过汽车将其提升出来。已知井底到井口的高度为3m,物体从井底到井口上升用时10s,汽车质量为1.2t,轮胎与地面的总接触面积为$800cm^2,$若四个车轮受力均匀,汽车前进过程中自身受到水平地面对它的摩擦力为车重的0.1倍(忽略绳的重力、绳与滑轮之间的摩擦,空气阻力不计)。
(1)求物体从井底到井口上升的平均速度。
(2)求未拖物体前汽车对水平地面的压强。
(3)把物体从井底匀速拖到井口的过程中,汽车的牵引力是多少?
(4)请算出汽车的牵引力做功的功率是多少?

(1)求物体从井底到井口上升的平均速度。
(2)求未拖物体前汽车对水平地面的压强。
(3)把物体从井底匀速拖到井口的过程中,汽车的牵引力是多少?
(4)请算出汽车的牵引力做功的功率是多少?

答案:
解:
(1)物体从井底到井口上升的平均速度:
$v=\frac{h}{t}=\frac{3\mathrm{m}}{10\mathrm{s}}=0.3\mathrm{m/s}$。
(2)汽车的重力:
$G_{车}=m_{车}g=1.2×10^{3}\mathrm{kg}×10\mathrm{N/kg}=1.2×10^{4}\mathrm{N}$,
未拖物体前汽车对水平地面的压力等于重力,则对地面的压强:
$p=\frac{F}{S}=\frac{G_{车}}{S}=\frac{1.2×10^{4}\mathrm{N}}{800×10^{-4}\mathrm{m^{2}}}=1.5×10^{5}\mathrm{Pa}$。
(3)汽车前进过程中受到的阻力:
$f=0.1G_{车}=0.1×1.2×10^{4}\mathrm{N}=1200\mathrm{N}$,
图中的滑轮为定滑轮,则物体匀速上升时,对汽车的拉力:
$F_{物}=G_{物}=2000\mathrm{N}$,
因为汽车匀速前进,受力平衡,则汽车的牵引力:
$F_{牵}=f+F_{物}=1200\mathrm{N}+2000\mathrm{N}=3200\mathrm{N}$。
(4)把物体从井底匀速拖到井口,汽车移动的距离$s_{车}=h=3\mathrm{m}$,
汽车的牵引力做的功:
$W=F_{牵}s_{车}=3200\mathrm{N}×3\mathrm{m}=9600\mathrm{J}$,
汽车的牵引力做功的功率:
$P=\frac{W}{t}=\frac{9600\mathrm{J}}{10\mathrm{s}}=960\mathrm{W}$。
(1)物体从井底到井口上升的平均速度:
$v=\frac{h}{t}=\frac{3\mathrm{m}}{10\mathrm{s}}=0.3\mathrm{m/s}$。
(2)汽车的重力:
$G_{车}=m_{车}g=1.2×10^{3}\mathrm{kg}×10\mathrm{N/kg}=1.2×10^{4}\mathrm{N}$,
未拖物体前汽车对水平地面的压力等于重力,则对地面的压强:
$p=\frac{F}{S}=\frac{G_{车}}{S}=\frac{1.2×10^{4}\mathrm{N}}{800×10^{-4}\mathrm{m^{2}}}=1.5×10^{5}\mathrm{Pa}$。
(3)汽车前进过程中受到的阻力:
$f=0.1G_{车}=0.1×1.2×10^{4}\mathrm{N}=1200\mathrm{N}$,
图中的滑轮为定滑轮,则物体匀速上升时,对汽车的拉力:
$F_{物}=G_{物}=2000\mathrm{N}$,
因为汽车匀速前进,受力平衡,则汽车的牵引力:
$F_{牵}=f+F_{物}=1200\mathrm{N}+2000\mathrm{N}=3200\mathrm{N}$。
(4)把物体从井底匀速拖到井口,汽车移动的距离$s_{车}=h=3\mathrm{m}$,
汽车的牵引力做的功:
$W=F_{牵}s_{车}=3200\mathrm{N}×3\mathrm{m}=9600\mathrm{J}$,
汽车的牵引力做功的功率:
$P=\frac{W}{t}=\frac{9600\mathrm{J}}{10\mathrm{s}}=960\mathrm{W}$。
查看更多完整答案,请扫码查看


