2025年暑假作业培优假期快乐练五年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业培优假期快乐练五年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
一、用天平称次品时,把下列数量的物品(每组只有一个稍轻的次品)分成3份,请在下面$□$内填写最简便的分法。
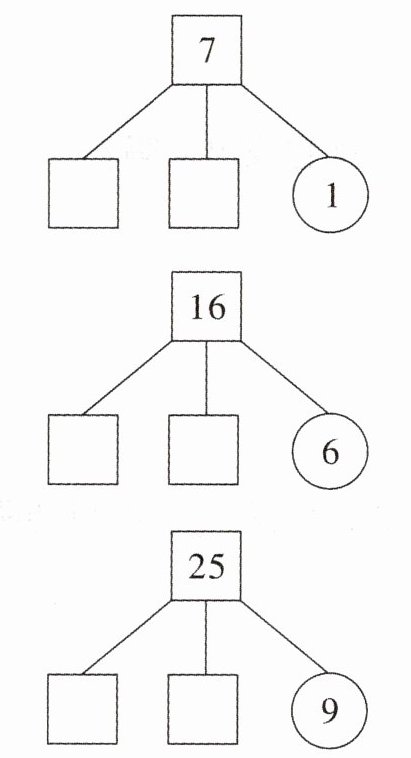

3 3
5 5
8 8
答案:
3 3
5 5
8 8
5 5
8 8
1. 有6瓶酸奶,其中一瓶质量不足,如果用无砝码的天平每次称2瓶,至少称(
2
)次才能保证找出这瓶次品。
答案:
解:
第一次:将6瓶酸奶分成3组,每组2瓶,任选两组放在天平两端。
- 若天平不平衡,次品在轻的那一组;
- 若天平平衡,次品在未称的那一组。
第二次:将含有次品的那一组2瓶酸奶分别放在天平两端,轻的一端即为次品。
至少称2次才能保证找出这瓶次品。
2
第一次:将6瓶酸奶分成3组,每组2瓶,任选两组放在天平两端。
- 若天平不平衡,次品在轻的那一组;
- 若天平平衡,次品在未称的那一组。
第二次:将含有次品的那一组2瓶酸奶分别放在天平两端,轻的一端即为次品。
至少称2次才能保证找出这瓶次品。
2
2. 从9件物品中找出其中的1件次品(次品略重或略轻),把9件物品平均分成(
3
)份称较为合适。
答案:
3
3. 在10个零件里有1个是次品(次品重一些),用无砝码的天平称,至少称(
3
)次就一定能找出次品。
答案:
解:
第一次:将10个零件分成3份(3,3,4),把两份3个的分别放在天平两端。
- 若天平平衡,次品在4个那份中;
- 若天平不平衡,次品在较重的3个那份中。
第二次:
- 若次品在4个中,将4个分成(1,1,2),把两份1个的放在天平两端。若平衡,次品在2个那份中;若不平衡,较重的那个是次品。
- 若次品在3个中,将3个分成(1,1,1),任取两个放在天平两端。若平衡,剩下的那个是次品;若不平衡,较重的那个是次品。
第三次:若次品在2个中,将这2个分别放在天平两端,较重的那个是次品。
至少称3次就一定能找出次品。
3
第一次:将10个零件分成3份(3,3,4),把两份3个的分别放在天平两端。
- 若天平平衡,次品在4个那份中;
- 若天平不平衡,次品在较重的3个那份中。
第二次:
- 若次品在4个中,将4个分成(1,1,2),把两份1个的放在天平两端。若平衡,次品在2个那份中;若不平衡,较重的那个是次品。
- 若次品在3个中,将3个分成(1,1,1),任取两个放在天平两端。若平衡,剩下的那个是次品;若不平衡,较重的那个是次品。
第三次:若次品在2个中,将这2个分别放在天平两端,较重的那个是次品。
至少称3次就一定能找出次品。
3
4. 有8瓶维生素C,其中一瓶少3片,如果用天平称,至少需要(
2
)次才能保证找到。
答案:
将8瓶维生素C分成3瓶、3瓶、2瓶三份。
第一次:把两份3瓶的分别放在天平两端。
情况一:天平平衡,则少3片的在剩下的2瓶中。第二次:把这2瓶分别放在天平两端,轻的一端即为少3片的那瓶。
情况二:天平不平衡,则少3片的在轻的那3瓶中。第二次:从这3瓶中任取2瓶,分别放在天平两端,若平衡,剩下的那瓶是少3片的;若不平衡,轻的一端是少3片的。
至少需要2次才能保证找到。
2
第一次:把两份3瓶的分别放在天平两端。
情况一:天平平衡,则少3片的在剩下的2瓶中。第二次:把这2瓶分别放在天平两端,轻的一端即为少3片的那瓶。
情况二:天平不平衡,则少3片的在轻的那3瓶中。第二次:从这3瓶中任取2瓶,分别放在天平两端,若平衡,剩下的那瓶是少3片的;若不平衡,轻的一端是少3片的。
至少需要2次才能保证找到。
2
5. 有5袋泥土样本,其中4袋质量相同,都是25克,有1袋少了3克,如果用天平称,至少称(
2
)次才能保证找到质量轻的那袋。
答案:
解:第一次,将5袋泥土分成2袋、2袋、1袋三份。把两份2袋的分别放在天平两端,若天平平衡,则剩下的1袋是轻的;若不平衡,轻的那袋在天平上升的一端的2袋中。
第二次,把天平上升一端的2袋分别放在天平两端,上升一端的那袋就是轻的。
至少称2次才能保证找到质量轻的那袋。
2
第二次,把天平上升一端的2袋分别放在天平两端,上升一端的那袋就是轻的。
至少称2次才能保证找到质量轻的那袋。
2
6. 灰太狼用一瓶变形药水(质量比纯净水要稍重一些)偷换了羊村的15瓶纯净水中的一瓶,聪明的喜羊羊至少要用无砝码的天平称(
3
)次才能保证找出这瓶变形药水。
答案:
解:将15瓶水分成5瓶、5瓶、5瓶三份。
第一次:天平两边各放5瓶,若平衡,则剩余5瓶中有变形药水;若不平衡,重的一边5瓶中有变形药水。
第二次:将有变形药水的5瓶分成2瓶、2瓶、1瓶三份,天平两边各放2瓶,若平衡,剩余1瓶为变形药水;若不平衡,重的一边2瓶中有变形药水。
第三次:将有变形药水的2瓶放在天平两边,重的一边为变形药水。
至少称3次才能保证找出这瓶变形药水。
3
第一次:天平两边各放5瓶,若平衡,则剩余5瓶中有变形药水;若不平衡,重的一边5瓶中有变形药水。
第二次:将有变形药水的5瓶分成2瓶、2瓶、1瓶三份,天平两边各放2瓶,若平衡,剩余1瓶为变形药水;若不平衡,重的一边2瓶中有变形药水。
第三次:将有变形药水的2瓶放在天平两边,重的一边为变形药水。
至少称3次才能保证找出这瓶变形药水。
3
三、在9颗螺丝钉中,混入了1颗不合格的螺丝钉(次品),它与合格螺丝钉的外形一模一样,只是质量略重一些,如果用天平称,至少称(
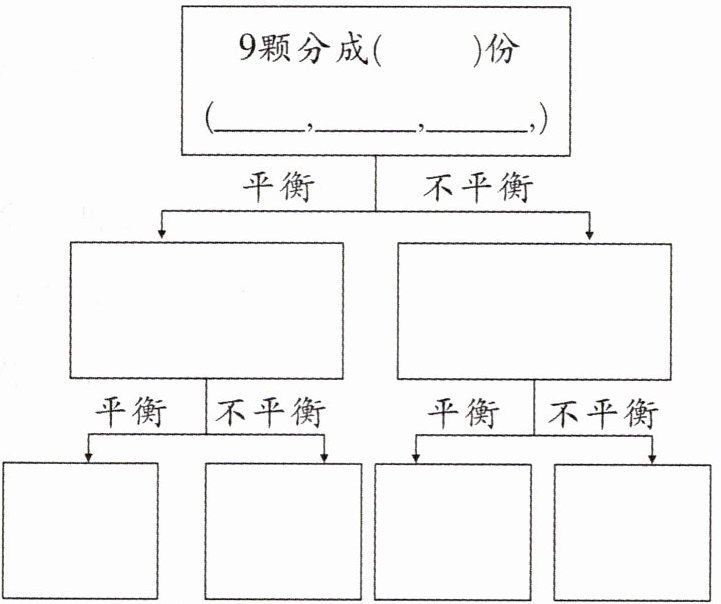
图示:9颗分成(
2
)次能保证找出这个次品。将下图补充完整。
图示:9颗分成(
3
)份;(3,3,3
);下面从左到右依次为:(3
);(3
);(1,1,1
);(1,1,1
);(1,1,1
);(1,1,1
) 。
答案:
解析:本题可根据找次品问题的最优策略,将物品尽量平均分成$3$份来逐步分析称重过程,进而确定至少称的次数并补充完整图示。
步骤一:分析至少称的次数
将$9$颗螺丝钉分成$3$份,每份$3$颗。
第一次称:把其中两份分别放在天平秤两端,若天平平衡,则次品在未取的$3$颗中;若不平衡,则次品在天平下沉的那$3$颗中。
第二次称:从有次品的$3$颗中任取$2$颗,分别放在天平秤两端,若天平平衡,则未取那颗是次品;若不平衡,天平下沉的一端就是次品。
所以至少称$2$次能保证找出这个次品。
步骤二:补充图示
第一次称:$9$颗分成$3$份,每份$3$颗,即$(3,3,3)$。
第二次称:
若第一次称天平平衡,从剩下$3$颗中再分成$3$份,每份$1$颗,即$(1,1,1)$,任取$2$颗称,平衡则剩下$1$颗是次品,不平衡则下沉那颗是次品。
若第一次称天平不平衡,从下沉的$3$颗中再分成$3$份,每份$1$颗,即$(1,1,1)$,任取$2$颗称,平衡则剩下$1$颗是次品,不平衡则下沉那颗是次品。
补充完整的图示如下:
```
9颗分成
(3)份
(3,3,3)
平衡 不平衡
| |
(3)
(3)
平衡 不平衡 平衡 不平衡
| | | |
(1,1,1) (1,1,1) (1,1,1) (1,1,1)
```
答案:$2$;图示:$9$颗分成$(3)$份;$(3,3,3)$;下面从左到右依次为:$(3)$;$(3)$;$(1,1,1)$;$(1,1,1)$;$(1,1,1)$;$(1,1,1)$ 。
步骤一:分析至少称的次数
将$9$颗螺丝钉分成$3$份,每份$3$颗。
第一次称:把其中两份分别放在天平秤两端,若天平平衡,则次品在未取的$3$颗中;若不平衡,则次品在天平下沉的那$3$颗中。
第二次称:从有次品的$3$颗中任取$2$颗,分别放在天平秤两端,若天平平衡,则未取那颗是次品;若不平衡,天平下沉的一端就是次品。
所以至少称$2$次能保证找出这个次品。
步骤二:补充图示
第一次称:$9$颗分成$3$份,每份$3$颗,即$(3,3,3)$。
第二次称:
若第一次称天平平衡,从剩下$3$颗中再分成$3$份,每份$1$颗,即$(1,1,1)$,任取$2$颗称,平衡则剩下$1$颗是次品,不平衡则下沉那颗是次品。
若第一次称天平不平衡,从下沉的$3$颗中再分成$3$份,每份$1$颗,即$(1,1,1)$,任取$2$颗称,平衡则剩下$1$颗是次品,不平衡则下沉那颗是次品。
补充完整的图示如下:
```
9颗分成
(3)份
(3,3,3)
平衡 不平衡
| |
(3)
(3)
平衡 不平衡 平衡 不平衡
| | | |
(1,1,1) (1,1,1) (1,1,1) (1,1,1)
```
答案:$2$;图示:$9$颗分成$(3)$份;$(3,3,3)$;下面从左到右依次为:$(3)$;$(3)$;$(1,1,1)$;$(1,1,1)$;$(1,1,1)$;$(1,1,1)$ 。
1. 方法一:每次天平两边各放一颗珍珠。若①处不平衡,则
2. 方法二:每次天平两边各放2颗珍珠。在①处一定
3. 方法一至少称
轻的
是次品;若②处不平衡了,则轻的
是次品;在③处一定不平衡
,轻的
是次品。2. 方法二:每次天平两边各放2颗珍珠。在①处一定
不平衡
,轻的
是次品;在②处一定不平衡
,轻的
是次品。3. 方法一至少称
3
次,可以保证找到次品;方法二至少称2次,可以保证找到次品,将被称的物品分成3
份,所用的次数要少。
答案:
1. 轻的 轻的 不平衡 轻的
2. 不平衡 轻的 不平衡 轻的
3. 3 3
2. 不平衡 轻的 不平衡 轻的
3. 3 3
查看更多完整答案,请扫码查看


