《2025年暑假生活安徽教育出版社数学通用版S》

17. 定义：从$∠α(90^{\circ} ＜ ∠α ＜ 180^{\circ})$的顶点出发,在角的内部作一条射线,若该射线将$∠α分得的两个角中有一个角与∠α$互为补角,则称该射线为$∠α$的“好线”。
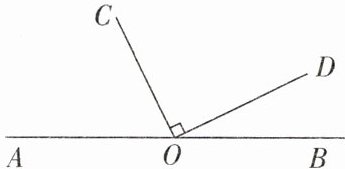
如图所示,点$O在直线AB$上,$OC$,$OD在直线AB$上方,且$OC⊥OD$,射线$OE是∠AOD$的“好线”。
(1)若$∠BOD = 26^{\circ}$,且$OE在∠COD$内部,则$∠COE = $____$^{\circ}$；
(2)若$OE恰好平分∠AOC$,请求出$∠BOD$的度数；
(3)若$OF是∠AOE$的平分线,$OG是∠BOC$的平分线,请画出图形,探究$∠EOF与∠DOG$的数量关系,并说明理由。

答案：
解：（1）64（2）若$OE$恰好平分$\angle AOC$，所以$\angle AOE=\angle COE=\angle BOD$。所以$\angle BOD=\frac{1}{3}×(180^{\circ}-90^{\circ})=30^{\circ}$。（3）如图①、图②所示，$\angle EOF+\angle DOG=45^{\circ}$或$\angle EOF=2\angle DOG$．理由如下：如图①所示，由于射线$OE$是$\angle AOD$的“好线”，当$\angle AOE+\angle AOD=180^{\circ}$时，因为$\angle AOD+\angle BOD=180^{\circ}$，所以$\angle AOE=\angle BOD$。因为$OF$是$\angle AOE$的平分线，所以$\angle EOF=\frac{1}{2}\angle AOE=\frac{1}{2}\angle BOD$。因为$OG$是$\angle BOC$的平分线，所以$\angle BOG=\frac{1}{2}\angle BOC=\frac{1}{2}×(90^{\circ}+\angle BOD)=45^{\circ}+\frac{1}{2}\angle BOD$。所以$\angle DOG=\angle BOG-\angle BOD=45^{\circ}-\frac{1}{2}\angle BOD$。所以$\angle EOF+\angle DOG=45^{\circ}$。如图②所示，由于射线$OE$是$\angle AOD$的“好线”，当$\angle DOE+\angle AOD=180^{\circ}$时，因为$\angle AOD+\angle BOD=180^{\circ}$，所以$\angle DOE=\angle BOD$。所以$\angle DOG=\frac{1}{2}\angle BOC-\angle BOD=\frac{1}{2}(90^{\circ}+\angle BOD)-\angle BOD=45^{\circ}-\frac{1}{2}\angle BOD$，$\angle EOF=\frac{1}{2}\angle AOE=\frac{1}{2}×(180^{\circ}-2\angle BOD)=90^{\circ}-\angle BOD$。所以$\angle EOF=2\angle DOG$。综上所述，$\angle EOF+\angle DOG=45^{\circ}$或$\angle EOF=2\angle DOG$。