6. 如图所示,直线$AB$,$CD相交于点O$,$OE⊥AB$.若$∠COE= 55^{\circ}$,则$∠AOD$的度数为(
A.$135^{\circ}$
B.$145^{\circ}$
C.$155^{\circ}$
D.$160^{\circ}$
B
)A.$135^{\circ}$
B.$145^{\circ}$
C.$155^{\circ}$
D.$160^{\circ}$
答案:
B
7. 如图所示,$CD是∠ECB$的平分线,且$CD// AB$,$∠B= 40^{\circ}$,则$∠ECD$的度数为(
A.$30^{\circ}$
B.$40^{\circ}$
C.$50^{\circ}$
D.$60^{\circ}$
B
)A.$30^{\circ}$
B.$40^{\circ}$
C.$50^{\circ}$
D.$60^{\circ}$
答案:
B
8. 如图所示,如果$∠1+∠2= 260^{\circ}$,则$∠3$的度数为
50°
.
答案:
50°
9. 如图所示,直线$a$,$b被直线c$所截,请添加一个条件

∠1=∠3
,使得$a// b$(只写出一种情况即可).
答案:
∠1=∠3(答案不唯一)
10. 如图所示,易拉罐的上下底面互相平行,吸管吸易拉罐内的饮料时,$∠1= 112^{\circ}$,则$∠2= $
68°
.
答案:
68°
11. 如图所示,直线$AB和直线CD相交于点O$,若$∠1+∠2= 90^{\circ}$,求$∠AOD$的度数.


答案:
解:因为∠1与∠2是对顶角,所以∠1=∠2。因为∠1+∠2=90°,所以∠1=∠2=45°。所以∠AOD=180°−∠1=135°。
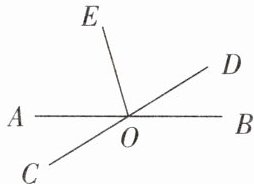
12. 如图所示,直线$AB和CD交于点O$,$OE平分∠AOD$,$∠AOC+∠BOD= 64^{\circ}$,求$∠BOE$的度数.

答案:
解:因为∠AOC与∠BOD是对顶角,∠AOC+∠BOD=64°,所以∠AOC=∠BOD=32°。所以∠AOD=180°−∠AOC=148°。因为OE平分∠AOD,所以∠DOE=$\frac{1}{2}$∠AOD=74°。所以∠BOE=∠BOD+∠DOE=32°+74°=106°。
13. 如图所示,已知$CA平分∠BCD$,$∠A= ∠BCA$.试说明:$AB// CD$.


答案:
解:因为CA平分∠BCD,所以∠ACD=∠BCA。因为∠A=∠BCA,所以∠A=∠ACD。所以AB//CD。
解:因为$∠3= ∠4$(已知),
所以
所以$∠5+$
因为$∠5= ∠6$(已知),所以$∠6+$
所以$AB// CD$(
所以$∠2= ∠EGA$(
因为$∠1= ∠2$(已知),所以$∠1= ∠EGA$(等量代换),
所以
所以
CF
//BD
(内错角相等,两直线平行
),所以$∠5+$
∠BAC
$=180^{\circ}$(两直线平行,同旁内角互补
).因为$∠5= ∠6$(已知),所以$∠6+$
∠BAC
$=180^{\circ}$(等量代换),所以$AB// CD$(
同旁内角互补,两直线平行
),所以$∠2= ∠EGA$(
两直线平行,同位角相等
).因为$∠1= ∠2$(已知),所以$∠1= ∠EGA$(等量代换),
所以
ED
//FB
(同位角相等,两直线平行
).
答案:
CF BD 内错角相等,两直线平行 ∠BAC 两直线平行,同旁内角互补 ∠BAC 同旁内角互补,两直线平行 两直线平行,同位角相等 ED FB 同位角相等,两直线平行
查看更多完整答案,请扫码查看


