《2025年暑假生活安徽教育出版社数学通用版S》

8. 已知正方形$ABCD的边长为a$,正方形$FGCH的边长为b$,长方形$ABGE和EFHD$为阴影部分,将图(1)中的长方形$ABGE和EFHD$剪下来,拼成如图(2)所示的长方形,比较图(2)与图(1)的阴影部分的面积,可得等式(A)
A.$(a + b)(a - b) = a^{2} - b^{2}$
B.$(a + b)^{2} = a^{2} + 2ab + b^{2}$
C.$(a - b)^{2} = a^{2} - 2ab + b^{2}$
D.$a(a + b) = a^{2} + ab$

答案： A

9. 因式分解：$x^{3} - 2x^{2} + x = $$x(x - 1)^2$。

答案： $x(x - 1)^2$

10. 如果关于$x的多项式4x^{2} + 6x + (2m - 1)^{2}$是完全平方式,那么$m = $$\frac{5}{4}$或$-\frac{1}{4}$。

答案： $\frac{5}{4}$或$-\frac{1}{4}$

11. 将关于$x的一次二项式ax + b与二次三项式x^{2} + 2x + 3$相乘,积中不出现一次项,且二次项系数为$1$,则$a + b = $$-1$。

答案： $-1$

12. 先因式分解,再计算求值：$4x(m - 2) - 3x(m - 2)^{2}$,其中$x = 1.5$,$m = 6$。

答案： 解：原式$ = (m - 2)[4x - 3x(m - 2)] = 4×(6 - 4.5×4) = -48 $。

13. 计算：
(1)$(2a^{2})^{2} - a^{7}÷(-a)^{3}$；
(2)$(x + 5)(x - 5) - (x + 2)^{2}$。

答案：
(1)$ (2a^2)^2 - a^7÷(-a)^3 = 4a^4 - a^7÷(-a^3) = 4a^4 + a^4 = 5a^4 $。
(2)$ (x + 5)(x - 5) - (x + 2)^2 = x^2 - 25 - (x^2 + 4x + 4) = x^2 - 25 - x^2 - 4x - 4 = -29 - 4x $。

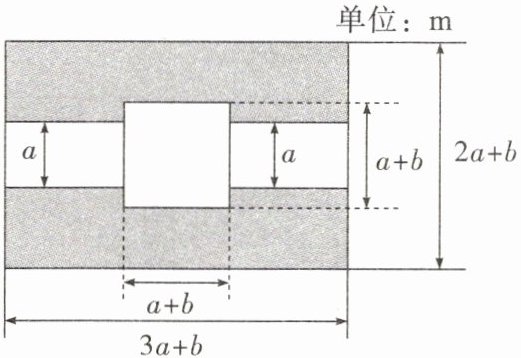
14. 如图所示,某市有一块长为$(3a + b)m$、宽为$(2a + b)m$的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为$a m的道路(a ＞ 0,b ＞ 0)$。
(1)试用含$a$,$b$的代数式表示绿化面积；
(2)若$a = 30$,$b = 20$,请求出绿化面积。

答案：
(1)绿化面积为$ (3a + b)(2a + b) - (a + b)^2 - a(3a + b - a - b) $
$ = 6a^2 + 5ab + b^2 - a^2 - 2ab - b^2 - 2a^2 $
$ = 3a^2 + 3ab(m^2) $。
答：绿化面积是$ (3a^2 + 3ab)m^2 $。
(2)当$ a = 30 $，$ b = 20 $时，
绿化面积是$ 3a^2 + 3ab = 3×900 + 3×30×20 = 4500(m^2) $。