2025年智趣暑假作业云南科技出版社八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智趣暑假作业云南科技出版社八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
3. 已知:如图,$BE$,$CF为\triangle ABC$的高,且$BE = CF$,$BE$,$CF交BE于点H$,若$BC = 10$,$FC = 8$,则$EC = $
6
。
答案:
6
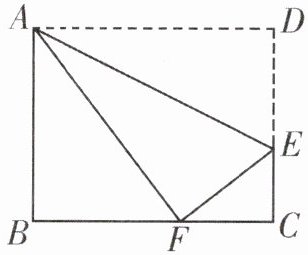
1. 如图所示,将长方形$ABCD沿AE$折叠,使点$D落在BC边的点F$处。已知$AB = 8\mathrm{cm}$,$BC = 10\mathrm{cm}$,求$EC$的长。

答案:
3 cm
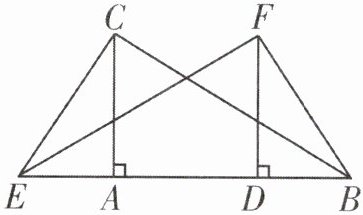
2. 如图,点$E$,$A$,$B$,$D$在同一直线上,$CA\perp EB于点A$,$FD\perp EB于点D$,$CA = FD$,$CE = FB$。
求证:$BC = EF$。
求证:$BC = EF$。

答案:
证明:
∵ $ CA \perp EB $,$ FD \perp EB $,
∴ $ \angle CAE = \angle FDB = 90^\circ $。
在 $ \text{Rt}\triangle CAE $ 和 $ \text{Rt}\triangle FDB $ 中,
$ CA = FD $,$ CE = FB $,
∴ $ \text{Rt}\triangle CAE \cong \text{Rt}\triangle FDB (\text{HL}) $。
∴ $ EA = DB $。
∵ $ E, A, B, D $ 在同一直线上,
∴ $ EA + AD = DB + AD $,即 $ ED = BA $。
在 $ \triangle CAB $ 和 $ \triangle FDE $ 中,
$ CA = FD $,$ \angle CAB = \angle FDE = 90^\circ $,$ BA = ED $,
∴ $ \triangle CAB \cong \triangle FDE (\text{SAS}) $。
∴ $ BC = EF $。
∵ $ CA \perp EB $,$ FD \perp EB $,
∴ $ \angle CAE = \angle FDB = 90^\circ $。
在 $ \text{Rt}\triangle CAE $ 和 $ \text{Rt}\triangle FDB $ 中,
$ CA = FD $,$ CE = FB $,
∴ $ \text{Rt}\triangle CAE \cong \text{Rt}\triangle FDB (\text{HL}) $。
∴ $ EA = DB $。
∵ $ E, A, B, D $ 在同一直线上,
∴ $ EA + AD = DB + AD $,即 $ ED = BA $。
在 $ \triangle CAB $ 和 $ \triangle FDE $ 中,
$ CA = FD $,$ \angle CAB = \angle FDE = 90^\circ $,$ BA = ED $,
∴ $ \triangle CAB \cong \triangle FDE (\text{SAS}) $。
∴ $ BC = EF $。
查看更多完整答案,请扫码查看


