2025年智趣暑假作业云南科技出版社八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智趣暑假作业云南科技出版社八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 已知实数 $ x,y,m $ 满足 $ \sqrt { x + 2 } + | 3 x + y + m | = 0 $,且 $ y $ 为负数,则 $ m $ 的取值范围是(
A.$ m > 6 $
B.$ m < 6 $
C.$ m > - 6 $
D.$ m < - 6 $
A
)A.$ m > 6 $
B.$ m < 6 $
C.$ m > - 6 $
D.$ m < - 6 $
答案:
【解析】:
题目考察了非负数的性质与一元一次不等式的求解。
由于$\sqrt{x + 2}$和$|3x + y + m|$都是非负数,且它们的和为0,
根据非负数的性质:几个非负数的和为0时,这几个非负数都为0。
所以我们可以得到以下两个方程:
$x + 2 = 0$,
$3x + y + m = 0$。
从第一个方程,我们可以得到:
$x = -2$。
将$x = -2$代入第二个方程,我们得到:
$3(-2) + y + m = 0$,
即$y = 6 - m$。
但题目给出$y$为负数,所以我们有:
$6 - m < 0$。
解这个不等式,我们得到:
$m > 6$。
【答案】:A. $m > 6$。
题目考察了非负数的性质与一元一次不等式的求解。
由于$\sqrt{x + 2}$和$|3x + y + m|$都是非负数,且它们的和为0,
根据非负数的性质:几个非负数的和为0时,这几个非负数都为0。
所以我们可以得到以下两个方程:
$x + 2 = 0$,
$3x + y + m = 0$。
从第一个方程,我们可以得到:
$x = -2$。
将$x = -2$代入第二个方程,我们得到:
$3(-2) + y + m = 0$,
即$y = 6 - m$。
但题目给出$y$为负数,所以我们有:
$6 - m < 0$。
解这个不等式,我们得到:
$m > 6$。
【答案】:A. $m > 6$。
2. 点 $ P ( 2 m - 1,3 ) $ 在第二象限,则 $ m $ 的取值范围是(
A.$ m > \frac { 1 } { 2 } $
B.$ m \geq \frac { 1 } { 2 } $
C.$ m < \frac { 1 } { 2 } $
D.$ m \leq \frac { 1 } { 2 } $
C
)A.$ m > \frac { 1 } { 2 } $
B.$ m \geq \frac { 1 } { 2 } $
C.$ m < \frac { 1 } { 2 } $
D.$ m \leq \frac { 1 } { 2 } $
答案:
【解析】:
题目要求确定点$P(2m-1,3)$在第二象限时,$m$的取值范围。
在第二象限,一个点的横坐标($x$坐标)必须小于0,而纵坐标($y$坐标)必须大于0。
对于点$P(2m-1,3)$,纵坐标已经给出为3,满足第二象限的条件(纵坐标大于0)。
接下来需要确定横坐标$2m-1$小于0的条件。
解不等式$2m-1 < 0$,得到:
$2m < 1$
$m < \frac{1}{2}$
根据这个不等式,可以确定$m$的取值范围是$m < \frac{1}{2}$。
【答案】:
C.$m < \frac { 1 } { 2 } $
题目要求确定点$P(2m-1,3)$在第二象限时,$m$的取值范围。
在第二象限,一个点的横坐标($x$坐标)必须小于0,而纵坐标($y$坐标)必须大于0。
对于点$P(2m-1,3)$,纵坐标已经给出为3,满足第二象限的条件(纵坐标大于0)。
接下来需要确定横坐标$2m-1$小于0的条件。
解不等式$2m-1 < 0$,得到:
$2m < 1$
$m < \frac{1}{2}$
根据这个不等式,可以确定$m$的取值范围是$m < \frac{1}{2}$。
【答案】:
C.$m < \frac { 1 } { 2 } $
3. 某种商品的进价为 $ 800 $ 元,出售时标价为 $ 1200 $ 元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于 $ 5 \% $,则最低可至(
A.$ 6 $ 折
B.$ 7 $ 折
C.$ 8 $ 折
D.$ 9 $ 折
B
)A.$ 6 $ 折
B.$ 7 $ 折
C.$ 8 $ 折
D.$ 9 $ 折
答案:
【解析】:
本题主要考察利润率的计算和打折销售问题的应用。
首先,我们需要明确几个关键概念:
进价:商品购进的价格,这里是800元。
标价:商品标出的销售价格,这里是1200元。
打折:在标价的基础上进行价格减免,如打x折,则售价为标价的$\frac{x}{10}$。
利润率:利润与进价的比值,即 $\text{利润率} = \frac{\text{利润}}{\text{进价}}$。
题目要求保证利润率不低于5%,即 $\text{利润率} \geq 5\%$。
利润可以用售价减去进价来计算,即 $\text{利润} = \text{售价} - \text{进价}$。
设商品打x折,则售价为 $1200 × \frac{x}{10}$。
根据利润率的定义,我们可以建立不等式:
$\frac{1200 × \frac{x}{10} - 800}{800} \geq 0.05$
解这个不等式,我们得到 $x \geq 7$。
因此,最低可以打7折。
【答案】:
B. 7折。
本题主要考察利润率的计算和打折销售问题的应用。
首先,我们需要明确几个关键概念:
进价:商品购进的价格,这里是800元。
标价:商品标出的销售价格,这里是1200元。
打折:在标价的基础上进行价格减免,如打x折,则售价为标价的$\frac{x}{10}$。
利润率:利润与进价的比值,即 $\text{利润率} = \frac{\text{利润}}{\text{进价}}$。
题目要求保证利润率不低于5%,即 $\text{利润率} \geq 5\%$。
利润可以用售价减去进价来计算,即 $\text{利润} = \text{售价} - \text{进价}$。
设商品打x折,则售价为 $1200 × \frac{x}{10}$。
根据利润率的定义,我们可以建立不等式:
$\frac{1200 × \frac{x}{10} - 800}{800} \geq 0.05$
解这个不等式,我们得到 $x \geq 7$。
因此,最低可以打7折。
【答案】:
B. 7折。
1. 在实数范围内定义一种新运算“$ \oplus $”,其运算规则为:$ a \oplus b = - 2 a + 3 b $。如:$ 1 \oplus 5 = - 2 × 1 + 3 × 5 = 13 $。则不等 $ x \oplus 4 < 0 $ 的解集为
$x > 6$
。
答案:
【解析】:
本题主要考察对新定义运算的理解以及不等式的求解。
根据题目中给出的新运算规则 $a \oplus b = -2a + 3b$,
首先,将$x \oplus 4$ 转化为标准的数学表达式:
$x \oplus 4 = -2x + 3 × 4 = -2x + 12$。
接下来,解不等式 $-2x + 12 < 0$:
移项得:$-2x < -12$,
除以-2(注意,当除以负数时,不等号方向要改变)得:$x > 6$。
【答案】:
$x > 6$。
本题主要考察对新定义运算的理解以及不等式的求解。
根据题目中给出的新运算规则 $a \oplus b = -2a + 3b$,
首先,将$x \oplus 4$ 转化为标准的数学表达式:
$x \oplus 4 = -2x + 3 × 4 = -2x + 12$。
接下来,解不等式 $-2x + 12 < 0$:
移项得:$-2x < -12$,
除以-2(注意,当除以负数时,不等号方向要改变)得:$x > 6$。
【答案】:
$x > 6$。
2. 已知关于 $ x $ 的不等式 $ 2 x - a > - 3 $ 的解集如图,则 $ a $ 的值为
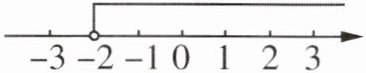
$-1$
。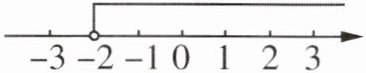
答案:
【解析】:
首先,我们解不等式$2x - a > -3$,
移项得,$2x > a - 3$,
然后,两边同时除以2,得到$x > \frac{a - 3}{2}$,
由题意知,这个不等式的解集与图示的解集相同,即$x > -2$,
因此,我们可以设置等式$\frac{a - 3}{2} = -2$,
接下来,我们解这个等式以求出$a$的值,
两边同时乘以2,得到$a - 3 = -4$,
移项得,$a = -4 + 3 = -1$。
【答案】:
$-1$
首先,我们解不等式$2x - a > -3$,
移项得,$2x > a - 3$,
然后,两边同时除以2,得到$x > \frac{a - 3}{2}$,
由题意知,这个不等式的解集与图示的解集相同,即$x > -2$,
因此,我们可以设置等式$\frac{a - 3}{2} = -2$,
接下来,我们解这个等式以求出$a$的值,
两边同时乘以2,得到$a - 3 = -4$,
移项得,$a = -4 + 3 = -1$。
【答案】:
$-1$
3. 在一次社会实践活动中,某班可筹集到的活动经费最多为 $ 900 $ 元,此次活动租车需 $ 300 $ 元,每个学生活动期间所需经费为 $ 15 $ 元,则参加这次活动的学生最多有
40
人。
答案:
【解析】:
这是一道一元一次不等式应用题,主要考查了如何根据给定的条件建立不等式,并求解得到最大整数解。
首先,从题目中我们可以提取到以下关键信息:
1. 总活动经费最多为900元。
2. 租车费用为300元。
3. 每个学生活动期间所需经费为15元。
设参加这次活动的学生人数为$x$人。
根据这些信息,我们可以建立以下不等式来表示活动经费的约束:
$15x + 300 \leq 900$
解这个不等式,我们可以找到满足条件的最大学生人数。
【答案】:
解:设参加这次活动的学生人数为$x$人。
根据题意,我们可以建立以下不等式:
$15x + 300 \leq 900$
移项得:
$15x \leq 600$
除以15得:
$x \leq 40$
所以,参加这次活动的学生最多有40人。
故答案为:40。
这是一道一元一次不等式应用题,主要考查了如何根据给定的条件建立不等式,并求解得到最大整数解。
首先,从题目中我们可以提取到以下关键信息:
1. 总活动经费最多为900元。
2. 租车费用为300元。
3. 每个学生活动期间所需经费为15元。
设参加这次活动的学生人数为$x$人。
根据这些信息,我们可以建立以下不等式来表示活动经费的约束:
$15x + 300 \leq 900$
解这个不等式,我们可以找到满足条件的最大学生人数。
【答案】:
解:设参加这次活动的学生人数为$x$人。
根据题意,我们可以建立以下不等式:
$15x + 300 \leq 900$
移项得:
$15x \leq 600$
除以15得:
$x \leq 40$
所以,参加这次活动的学生最多有40人。
故答案为:40。
查看更多完整答案,请扫码查看


