2025年亮点给力提优课时作业本五年级数学上册苏教版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年亮点给力提优课时作业本五年级数学上册苏教版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
例1 你知道下面多边形的内角和是多少吗?

我的思考 因为三角形的内角和是 $ 180 ^ { \circ } $,所以我们可以根据三角形的内角和来探索其他多边形的内角和。如下图,从某个顶点出发作对角线,将多边形分割成三角形。

从图中可以看出,每个多边形的内角和都转化成了几个三角形的内角和之和。让我们来列个表观察、比较一下:
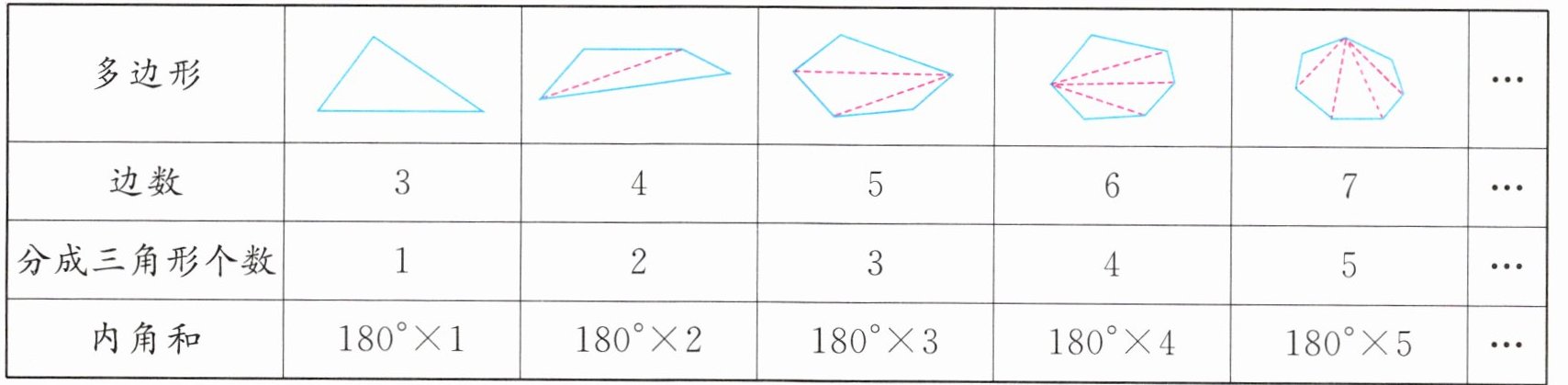
从表中可以发现,转化成的三角形的个数总比多边形的边数少 2,所以求多边形的内角和可以先用边数减 2 求出分割成的三角形的个数,再乘 $ 180 ^ { \circ } $ 就可以了。

我的思考 因为三角形的内角和是 $ 180 ^ { \circ } $,所以我们可以根据三角形的内角和来探索其他多边形的内角和。如下图,从某个顶点出发作对角线,将多边形分割成三角形。

从图中可以看出,每个多边形的内角和都转化成了几个三角形的内角和之和。让我们来列个表观察、比较一下:

从表中可以发现,转化成的三角形的个数总比多边形的边数少 2,所以求多边形的内角和可以先用边数减 2 求出分割成的三角形的个数,再乘 $ 180 ^ { \circ } $ 就可以了。
答案:
解析:本题考查通过将多边形分割成三角形来探究多边形内角和的规律。
解题步骤:
从表中可知,对于边数为$n$的多边形,其内角和的计算公式为$(n - 2)×180^{\circ}$。
假设多边形边数为$n$,根据上述规律,其内角和为$(n - 2)×180^{\circ}$。
答案:多边形内角和为$(n - 2)×180^{\circ}$($n$为多边形边数且$n\geqslant 3$且$n$为整数)。
解题步骤:
从表中可知,对于边数为$n$的多边形,其内角和的计算公式为$(n - 2)×180^{\circ}$。
假设多边形边数为$n$,根据上述规律,其内角和为$(n - 2)×180^{\circ}$。
答案:多边形内角和为$(n - 2)×180^{\circ}$($n$为多边形边数且$n\geqslant 3$且$n$为整数)。
活学活用 你知道十二边形的内角和是多少吗?
我的发现 多边形的内角和可以用“$ 180 ^ { \circ } × ( $ )”来计算。
我的发现 多边形的内角和可以用“$ 180 ^ { \circ } × ( $ )”来计算。
答案:
活学活用:180°×(12 - 2)=1800° 我的发现:边数$-2$
查看更多完整答案,请扫码查看


