第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
例1 巧算:$599999+49999+3999+299+19+5$。
思路点拨 遇到多个加数连加时,先观察算式中数据的特点。

“要灵活运用加法运算哟!”
可以将加数凑成整十、整百、整千、整万等的数,灵活运用加法交换律和加法结合律进行简便计算。
思路点拨 遇到多个加数连加时,先观察算式中数据的特点。

“要灵活运用加法运算哟!”
可以将加数凑成整十、整百、整千、整万等的数,灵活运用加法交换律和加法结合律进行简便计算。
答案:
例1 $ 599999 + 49999 + 3999 + 299 + 19 + 5 $
$ = (599999 + 1) + (49999 + 1) + $
$ (3999 + 1) + (299 + 1) + (19 + 1) $
$ = 600000 + 50000 + 4000 + 300 + 20 $
$ = 654320 $
![img alt=例1]
$ = (599999 + 1) + (49999 + 1) + $
$ (3999 + 1) + (299 + 1) + (19 + 1) $
$ = 600000 + 50000 + 4000 + 300 + 20 $
$ = 654320 $
![img alt=例1]
1. 巧算。
(1)$9+19+29+39+49+59+6$
(2)$99999+9998+997+96+10$
(3)$298+297+296+295+294$
例2 用简便方法计算。
(1)$128×4+64×12$ (2)$36×24+72×88$
思路点拨 这两道算式都是两个积的和的形式,如果乘数中有存在倍数关系的数,那么就可以先转化出相同的乘数,再用乘法分配律进行简便计算。
(1)$\underline{128×4}+\underline{64×12}$ (2)$\underline{36×24}+\underline{72×88}$
$\underline{64×2}$ $\underline{36×2×12}$
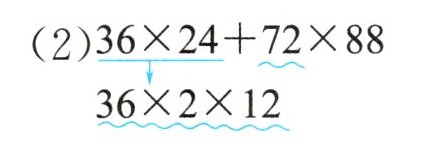
(1)$9+19+29+39+49+59+6$
(2)$99999+9998+997+96+10$
(3)$298+297+296+295+294$
例2 用简便方法计算。
(1)$128×4+64×12$ (2)$36×24+72×88$
思路点拨 这两道算式都是两个积的和的形式,如果乘数中有存在倍数关系的数,那么就可以先转化出相同的乘数,再用乘法分配律进行简便计算。
(1)$\underline{128×4}+\underline{64×12}$ (2)$\underline{36×24}+\underline{72×88}$
$\underline{64×2}$ $\underline{36×2×12}$
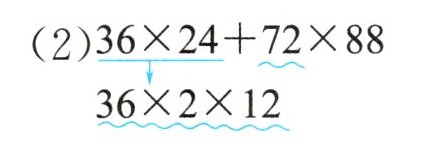
答案:
举一反三
1.
(1)210
(2)111100
(3)1480
1.
(1)210
(2)111100
(3)1480
查看更多完整答案,请扫码查看


