2025年奔跑吧少年九年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年奔跑吧少年九年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
15. (8分)如图,在正方形网格中,四边形$TABC的顶点坐标分别为T(1,1)$,$A(2,3)$,$B(3,3)$,$C(4,2)$.
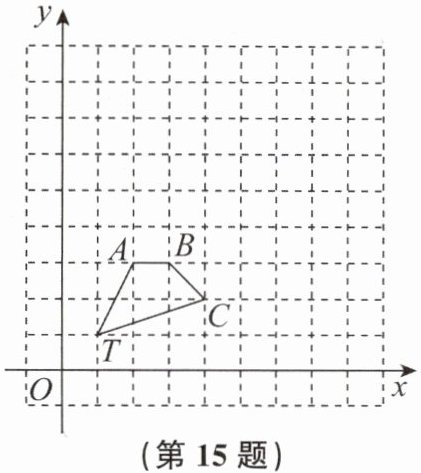
(1)以点$T(1,1)$为位似中心,在位似中心的同侧将四边形$TABC$放大为原来的2倍,放大后点$A$,$B$,$C的对应点分别为A'$,$B'$,$C'$,试画出四边形$TA'B'C'$.
(2)请写出点$A'$,$B'$,$C'$的坐标.
(3)在(1)中,若$D(a,b)为线段AC$上任一点,则变化后点$D的对应点D'$的坐标为______.
(1) 画图步骤:连接$TA$,$TB$,$TC$。延长$TA$到$A'$,使$TA' = 2TA$;延长$TB$到$B'$,使$TB' = 2TB$;延长$TC$到$C'$,使$TC' = 2TC$。顺次连接$TA'$,$A'B'$,$B'C'$,$C'T$,得到四边形$TA'B'C'$。
(2)$A'(3,5)$,$B'(5,5)$,$C'(7,3)$
(3)$(2a - 1,2b - 1)$

(1)以点$T(1,1)$为位似中心,在位似中心的同侧将四边形$TABC$放大为原来的2倍,放大后点$A$,$B$,$C的对应点分别为A'$,$B'$,$C'$,试画出四边形$TA'B'C'$.
(2)请写出点$A'$,$B'$,$C'$的坐标.
(3)在(1)中,若$D(a,b)为线段AC$上任一点,则变化后点$D的对应点D'$的坐标为______.
(1) 画图步骤:连接$TA$,$TB$,$TC$。延长$TA$到$A'$,使$TA' = 2TA$;延长$TB$到$B'$,使$TB' = 2TB$;延长$TC$到$C'$,使$TC' = 2TC$。顺次连接$TA'$,$A'B'$,$B'C'$,$C'T$,得到四边形$TA'B'C'$。
(2)$A'(3,5)$,$B'(5,5)$,$C'(7,3)$
(3)$(2a - 1,2b - 1)$
答案:
1. (1)**画图步骤**:
连接$TA$,$TB$,$TC$。
延长$TA$到$A'$,使$TA' = 2TA$;延长$TB$到$B'$,使$TB' = 2TB$;延长$TC$到$C'$,使$TC' = 2TC$。
顺次连接$TA'$,$A'B'$,$B'C'$,$C'T$,得到四边形$TA'B'C'$。(由于是画图题,这里文字描述画图过程)
2. (2)**求$A'$,$B'$,$C'$的坐标**:
已知$T(1,1)$,$A(2,3)$,$B(3,3)$,$C(4,2)$。
设点$P(x,y)$以$T(m,n)$为位似中心,位似比为$k$(同侧放大),则位似变换公式为$\left\{\begin{array}{l}x'=m + k(x - m)\\y'=n + k(y - n)\end{array}\right.$,这里$k = 2$,$m = 1$,$n = 1$。
对于$A(2,3)$:
$x_{A'}=1+2×(2 - 1)=3$,$y_{A'}=1+2×(3 - 1)=5$,所以$A'(3,5)$。
对于$B(3,3)$:
$x_{B'}=1+2×(3 - 1)=5$,$y_{B'}=1+2×(3 - 1)=5$,所以$B'(5,5)$。
对于$C(4,2)$:
$x_{C'}=1+2×(4 - 1)=7$,$y_{C'}=1+2×(2 - 1)=3$,所以$C'(7,3)$。
3. (3)**求$D'$的坐标**:
已知$D(a,b)$,根据位似变换公式$\left\{\begin{array}{l}x'=1+2×(a - 1)=2a - 1\\y'=1+2×(b - 1)=2b - 1\end{array}\right.$,所以$D'$的坐标为$(2a - 1,2b - 1)$。
综上,(2)$A'(3,5)$,$B'(5,5)$,$C'(7,3)$;(3)$(2a - 1,2b - 1)$。
连接$TA$,$TB$,$TC$。
延长$TA$到$A'$,使$TA' = 2TA$;延长$TB$到$B'$,使$TB' = 2TB$;延长$TC$到$C'$,使$TC' = 2TC$。
顺次连接$TA'$,$A'B'$,$B'C'$,$C'T$,得到四边形$TA'B'C'$。(由于是画图题,这里文字描述画图过程)
2. (2)**求$A'$,$B'$,$C'$的坐标**:
已知$T(1,1)$,$A(2,3)$,$B(3,3)$,$C(4,2)$。
设点$P(x,y)$以$T(m,n)$为位似中心,位似比为$k$(同侧放大),则位似变换公式为$\left\{\begin{array}{l}x'=m + k(x - m)\\y'=n + k(y - n)\end{array}\right.$,这里$k = 2$,$m = 1$,$n = 1$。
对于$A(2,3)$:
$x_{A'}=1+2×(2 - 1)=3$,$y_{A'}=1+2×(3 - 1)=5$,所以$A'(3,5)$。
对于$B(3,3)$:
$x_{B'}=1+2×(3 - 1)=5$,$y_{B'}=1+2×(3 - 1)=5$,所以$B'(5,5)$。
对于$C(4,2)$:
$x_{C'}=1+2×(4 - 1)=7$,$y_{C'}=1+2×(2 - 1)=3$,所以$C'(7,3)$。
3. (3)**求$D'$的坐标**:
已知$D(a,b)$,根据位似变换公式$\left\{\begin{array}{l}x'=1+2×(a - 1)=2a - 1\\y'=1+2×(b - 1)=2b - 1\end{array}\right.$,所以$D'$的坐标为$(2a - 1,2b - 1)$。
综上,(2)$A'(3,5)$,$B'(5,5)$,$C'(7,3)$;(3)$(2a - 1,2b - 1)$。
16. (10分)某小区为了促进生活垃圾的分类处理,将生活垃圾分为厨余、可回收和其他三类,分别记为$a$,$b$,$c$,并且设置了相应的垃圾箱,“厨余垃圾”箱、“可回收物”箱和“其他垃圾”箱,分别记为$A$,$B$,$C$.
(1)若将三类垃圾分别投入三类垃圾箱(每类垃圾箱都有垃圾投入),请用画树状图的方法求垃圾投放全部正确的概率.
(2)为调查居民生活垃圾分类投放情况,现随机抽取了该小区三类垃圾箱中总1000千克生活垃圾,数据统计如下(单位:千克):
| | $A$ | $B$ | $C$ |
| $a$ | 400 | 100 | 100 |
| $b$ | 30 | 240 | 30 |
| $c$ | 20 | 20 | 60 |
试估计厨余垃圾投放正确的概率.
(1)若将三类垃圾分别投入三类垃圾箱(每类垃圾箱都有垃圾投入),请用画树状图的方法求垃圾投放全部正确的概率.
(2)为调查居民生活垃圾分类投放情况,现随机抽取了该小区三类垃圾箱中总1000千克生活垃圾,数据统计如下(单位:千克):
| | $A$ | $B$ | $C$ |
| $a$ | 400 | 100 | 100 |
| $b$ | 30 | 240 | 30 |
| $c$ | 20 | 20 | 60 |
试估计厨余垃圾投放正确的概率.
答案:
(1)$\frac{1}{6}$。
(2)$\frac{2}{3}$。
(1)$\frac{1}{6}$。
(2)$\frac{2}{3}$。
17. (12分)如图,已知锐角三角形$ABC的外心为O$,线段$OA和BC的中点分别为M$,$N$.若$\angle ABC= 4\angle OMN$,$\angle ACB= 6\angle OMN$.求$\angle OMN$的度数.
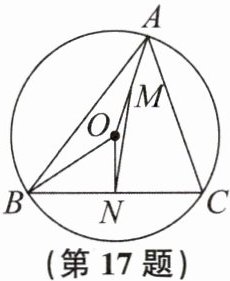

答案:
$12^{\circ}$。
18. (14分)如图,抛物线$y= x^{2}-x-1与y轴交于点C$,以原点$O$为圆心,$OC的长为半径作\odot O$,交$x轴于A$,$B$两点,交$y轴于另一点D$.设点$P为抛物线y= x^{2}-x-1$上的一点,作$PM\perp x轴于点M$,求使$\triangle PMB\backsim\triangle ADB时的点P$的坐标.


答案:
$(0,-1)$,$(2,1)$,$(\sqrt{2},1 - \sqrt{2})$,$(-\sqrt{2},1 + \sqrt{2})$。
查看更多完整答案,请扫码查看


