《2025年奔跑吧少年九年级数学全一册浙教版》

15. (8分)计算.
(1)$\frac {\sqrt {3}}{3}tan60^{\circ }-\frac {\sqrt {2}}{2}cos45^{\circ }$.
(2)$cos^{2}30^{\circ }+sin^{2}30^{\circ }-tan45^{\circ }$.

答案： （1）$\frac{1}{2}$. （2）0.

16. (10分)阳光中学选拔学生,最终选出男、女各一名组成搭档,去参加市里举办的学生才艺比赛.目前三个年级都有男、女各一名选手进入选拔,初一年级选手编号为男1号、女1号,初二年级选手编号为男2号、女2号,初三年级选手编号为男3号、女3号.
(1)请用列举法说明所有可能出现的结果.
(2)求同一年级男、女选手组成搭档的概率.
(3)求高年级男选手与低年级女选手组成搭档的概率.

答案： （1）男1号，女1号；男1号，女2号；男1号，女3号；男2号，女1号；男2号，女2号；男2号，女3号；男3号，女1号；男3号，女2号；男3号，女3号. （2）$\frac{1}{3}$. （3）$\frac{1}{3}$.

17. (12分)在平面直角坐标系中,$O$为坐标原点,二次函数$y= x^{2}+bx+c$($b,c$是常数)的图象与$x轴交于A,B$两点,与$y轴交于点C$,已知$B(1,0)$.
(1)若$A(0,0)$,求该二次函数的最小值.
(2)求证:$OA= OC$.
(3)若点$A位于点O,B$之间,求证:$-3\lt 2b+c\lt -2$.

答案：

（1）解：因为二次函数$y=x^2 + bx + c$的图象过$A(0,0)$和$B(1,0)$，将$A(0,0)$代入得$c=0$，将$B(1,0)$代入得$1 + b + 0 = 0$，解得$b=-1$，所以函数解析式为$y=x^2 - x$。化为顶点式$y=(x - \frac{1}{2})^2 - \frac{1}{4}$，所以该二次函数的最小值为$-\frac{1}{4}$。

（2）证明：设$A(x_1,0)$，因为二次函数$y=x^2 + bx + c$与$x$轴交于$A$、$B(1,0)$两点，所以$x_1$和$1$是方程$x^2 + bx + c = 0$的两根，由韦达定理得$x_1 × 1 = c$，即$x_1 = c$，所以$OA = |x_1| = |c|$。又因为点$C$是二次函数与$y$轴交点，令$x=0$，得$y=c$，所以$OC = |c|$，故$OA = OC$。

（3）证明：因为点$A$位于点$O$、$B$之间，所以$0 ＜ x_1 ＜ 1$（$x_1$为点$A$的横坐标），由（2）知$x_1 = c$，所以$0 ＜ c ＜ 1$。又由韦达定理得$x_1 + 1 = -b$，即$b = - (x_1 + 1)$，因为$0 ＜ x_1 ＜ 1$，所以$-2 ＜ b ＜ -1$。则$2b + c = 2(-x_1 - 1) + x_1 = -x_1 - 2$，因为$0 ＜ x_1 ＜ 1$，所以$-1 ＜ -x_1 ＜ 0$，所以$-3 ＜ -x_1 - 2 ＜ -2$，即$-3 ＜ 2b + c ＜ -2$。

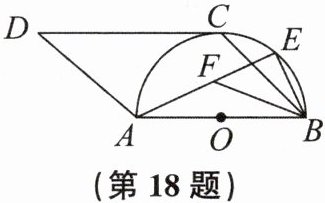
18. (14分)如图,$AB为半圆O$的直径,四边形$ABCD$为平行四边形,$E为\overset{\frown }{BC}$的中点,$BF平分∠ABC$,交$AE于点F$.
(1)求证:$BE= EF$.
(2)若$AB= 10,BF= 2\sqrt {10}$,求$AD$的长.

答案：

（1）证明：

∵AB是半圆O的直径，

∴∠AEB=90°，

∵E为$\widehat{BC}$的中点，

∴∠BAE=∠CBE，

∵BF平分∠ABC，

∴∠ABF=∠CBF，

∵∠EFB=∠BAE+∠ABF，∠EBF=∠CBE+∠CBF，

∴∠EFB=∠EBF，

∴BE=EF.

（2）8.