《2025年奔跑吧少年九年级数学全一册浙教版》

1. 已知$\odot O$的半径为3,圆心O到直线l的距离为2,则直线l与$\odot O$的位置关系是(A)
A.相交
B.相切
C.相离
D.不能确定

答案： A

2. 如图,在$Rt△ABC$中,$∠C= 90^{\circ },BC= 3,AC= 4$,则$tanB$的值为(D)
A.$\frac {4}{5}$
B.$\frac {3}{5}$
C.$\frac {3}{4}$
D.$\frac {4}{3}$

答案： D

3. 已知$△ABC\backsim △DEF,∠A= 35^{\circ },∠F= 80^{\circ }$,则$∠B$的度数为(A)
A.$65^{\circ }$
B.$75^{\circ }$
C.$80^{\circ }$
D.$35^{\circ }$

答案： A

4. 如图,$\widehat {MN}$的圆心为O,C,D两点三等分$\widehat {MN}$,连结MN,CD,下列结论中,错误的是(D)
A.$∠COM= ∠COD$
B.若$OM= MN$,则$∠AOB= 20^{\circ }$
C.$MN// CD$
D.$MN= 3CD$

答案： D

5. 如图,两条不平行的直线$l_{1}与直线l_{2}$相交于点O,四条平行线分别交直线$l_{1}$于点A,B,C,D,分别交直线$l_{2}于点A_{1},B_{1},C_{1},D_{1}$,则有$AA_{1}// BB_{1}// CC_{1}// DD_{1}$.如果$A_{1}O= 3,OB_{1}= B_{1}C_{1}= 2,C_{1}D_{1}= 4$,那么在下列结果中,线段之差最大的是(D)
A.$BD-AB$
B.$OC-OA$
C.$OC-CD$
D.$CD-OB$

答案： D

6. 将正六边形ABCDEF折叠成三角形后(如图①)用剪刀剪下一个角,展开后得到如图②所示的图形,图②中虚线为折叠时产生的折痕,折痕$AG+BH= AB$.若剪完后所得阴影图形的面积为原正六边形面积的$\frac {5}{6}$,则$\frac {GH}{AB}$的值为(A)
A.$\frac {\sqrt {2}}{2}$
B.$\frac {\sqrt {5}}{5}$
C.$\frac {1}{2}$
D.$\frac {2}{3}$

答案： A

7. 九(1)班将在3月5日开展“学雷锋”活动,需将全班同学分为“社区服务”“雷锋精神宣传”“爱心义卖”“线上公益”四个小组.每名同学被分到每个小组的可能性相等,则小星被分到“爱心义卖”小组的概率是$\frac{1}{4}$.

答案： $\frac{1}{4}$

8. 如图,要使$△AFE\backsim △ABC$,需要补充一个条件可以是$∠AEF = ∠ACB$（答案不唯一）(只需要填写一个即可).

答案： $∠AEF = ∠ACB$（答案不唯一）

9. 如图,已知$△ABC$的三个顶点均在格点上,则$cosA$的值为$\frac{2\sqrt{5}}{5}$.

答案： $\frac{2\sqrt{5}}{5}$

10. $△ABC$的内切圆的三个切点分别为D,E,F,连结OD,OE,OF,$∠A= 75^{\circ },∠B= 45^{\circ }$,则$∠EOF= $$120^{\circ}$.

答案： $120^{\circ}$

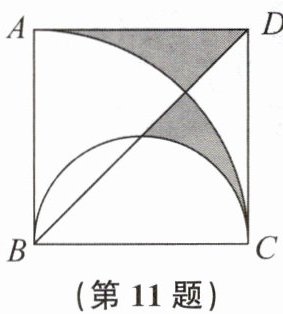
11. 如图,在正方形ABCD中,BD为对角线,以点B为圆心,AB为半径画弧,再以BC为直径画半圆.若$AB= 4$,则阴影部分的面积为$6 - π$(结果保留π).

答案： $6 - π$

12. 如图,抛物线$y= x^{2}+bx-3$的图象与x轴正半轴交于点A,与y轴交于点B,且$OA= 1$.
(1)$b=$2.
(2)已知P为该抛物线上一点,且设其横坐标为$t(t＜0)$,记该抛物线在点B与点P之间(包含点B和点P)这部分图象的最高点和最低点到x轴的距离分别为$d_{1},d_{2}$.若$|d_{1}-d_{2}|= 1$,则t的取值范围是$-2 ≤ t ≤ -1$ 或 $t = -4$ 或 $t = -\sqrt{7} - 1$.

答案：
(1) 2
(2) $-2 ≤ t ≤ -1$ 或 $t = -4$ 或 $t = -\sqrt{7} - 1$