《2025年奔跑吧少年九年级数学全一册浙教版》

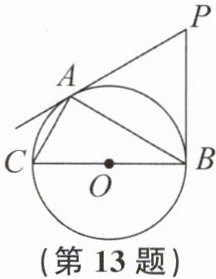
13. (8分)如图,PA,PB分别与$\odot O$相切于点A,B,AC为弦,BC为$\odot O$的直径.若$∠P= 60^{\circ },PB= 2cm$.
(1)求证:$△PAB$是等边三角形.
(2)求AC的长.

答案：

(1) 证明：
∵PA，PB分别与⊙O相切于点A，B，

∴PA=PB，

∵∠P=60°，

∴△PAB是等边三角形。

(2) $\frac{2\sqrt{3}}{3}$ cm.

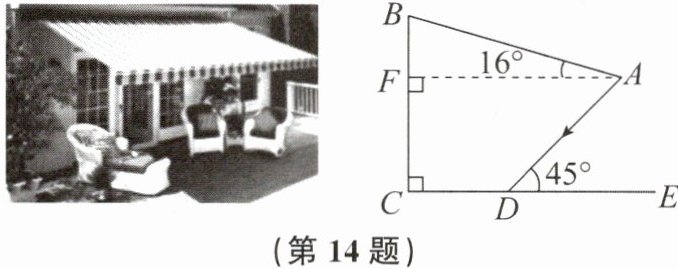
14. (10分)为建设美好公园社区,增强民众生活幸福感,某社区服务中心在文化活动室墙外安装避阳篷,便于社区居民休憩.如图,在侧面示意图中,$AF⊥BC$,遮阳篷AB长为5m,与水平面的夹角为$16^{\circ }$,且靠墙端离地高BC为4m,当太阳光线AD与地面CE的夹角为$45^{\circ }$时,求:
(1)BF的长.
(2)阴影CD的长.
(参考数据:$sin16^{\circ }\approx 0.28,cos16^{\circ }\approx 0.96,tan16^{\circ }\approx 0.29)$

答案：
(1) 1.4 m.
(2) 2.2 m.

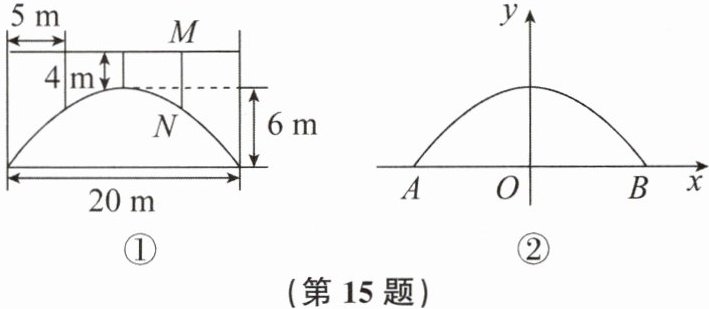
15. (10分)如图①,有一座桥拱为抛物线形的拱桥,在正常水位时,桥下的水面宽20m,拱顶到水面的距离为6m,到桥面的距离为4m,相邻两支柱间的距离均为5m,建立直角坐标系如图②所示.
(1)求抛物线的函数表达式.
(2)求支柱MN的长.
(3)随着水位的上升,桥下水面的宽度逐渐减小.一艘货船在水面上的部分的横截面是边长为5m的正方形,当水位上升0.75m时,这艘货船能否顺利通过拱桥?请说说你的理由.

答案：
(1) $y = -\frac{3}{50}x^{2} + 6$.
(2) 5.5 m.
(3) 不能

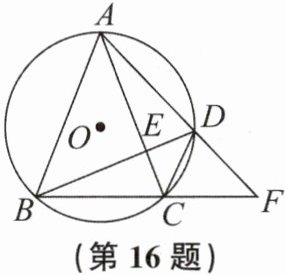
16. (12分)如图,等腰三角形ABC内接于$\odot O,AB= AC$.D为$\widehat {AC}$上一点,连结BD交AC于点E,连结AD并延长交BC的延长线于点F,连结CD.
(1)求证:$△CDF\backsim △ABF$.
(2)若$BD⊥AC$,
①求证:$∠BAC= 2∠CAF$;
②当$\frac {AB}{BC}= \frac {\sqrt {10}}{2}$时,求$\frac {S_{△CDF}}{S_{△ABF}}$的值.

答案： 1. （1）证明：
因为$AB = AC$，所以$\angle ABC=\angle ACB$。
又因为$\angle ADB=\angle ACB$（同弧所对的圆周角相等），$\angle ADB + \angle CDF=180^{\circ}$，$\angle ACB+\angle ACF = 180^{\circ}$，所以$\angle CDF=\angle ABC$。
因为$\angle F=\angle F$，所以$\triangle CDF\backsim\triangle ABF$（两角分别相等的两个三角形相似）。
2. （2）①证明：
因为$BD\perp AC$，$AB = AC$，所以$BD$平分$AC$（等腰三角形三线合一），即$BD$是$AC$的垂直平分线。
所以$AD = CD$，则$\angle CAD=\angle ACD$。
设$\angle CAF=\alpha$，则$\angle ADB=\angle ACB=\angle ABC$。
因为$\angle ADB=\angle CAD+\angle ACD = 2\angle CAD$，$\angle BAC=\angle BAD+\angle CAD$，又$\angle BAD=\angle BCD$（同弧所对的圆周角相等），$\angle BCD=\angle ADB$（同弧所对的圆周角相等）。
所以$\angle BAC = 2\angle CAF$。
3. （2）②解：
设$AB=\sqrt{10}x$，$BC = 2x$。
过$A$作$AH\perp BC$于$H$，因为$AB = AC$，所以$BH=\frac{1}{2}BC=x$。
在$Rt\triangle ABH$中，$AH=\sqrt{AB^{2}-BH^{2}}=\sqrt{(\sqrt{10}x)^{2}-x^{2}} = 3x$。
因为$\triangle CDF\backsim\triangle ABF$，所以$\frac{S_{\triangle CDF}}{S_{\triangle ABF}}=\left(\frac{CD}{AB}\right)^{2}$。
因为$\angle BAC = 2\angle CAF$，$\angle BAC+\angle ABC+\angle ACB = 180^{\circ}$，$\angle ABC=\angle ACB$，$\angle CAF=\angle CAD$，设$\angle CAF=\theta$，则$\angle BAC = 2\theta$，$2\theta + 2(2\theta)=180^{\circ}$（$\angle ACB=\angle ADB = 2\theta$），解得$\theta = 30^{\circ}$，$\angle BAC = 60^{\circ}$，$\triangle ABC$是等边三角形（$AB = AC$且$\angle BAC = 60^{\circ}$），则$AB = BC$，这与已知矛盾，我们换一种方法。
因为$\triangle CDF\backsim\triangle ABF$，$\frac{S_{\triangle CDF}}{S_{\triangle ABF}}=\left(\frac{CD}{AB}\right)^{2}$。
由$BD\perp AC$，$AB = AC$，设$AE = CE = a$。
因为$\angle CAF=\angle CBD$（同弧所对的圆周角相等），$\angle AEC=\angle BED = 90^{\circ}$。
又$\frac{AB}{BC}=\frac{\sqrt{10}}{2}$，设$AB=\sqrt{10}k$，$BC = 2k$。
因为$\triangle CDF\backsim\triangle ABF$，根据相似三角形面积比等于相似比的平方。
由$\angle BAC = 2\angle CAF$，$\angle ABD=\angle CBD$（等腰三角形三线合一）。
设$\angle CAF=\alpha$，$\angle BAC = 2\alpha$，$\angle ABC=\angle ACB = 90^{\circ}-\alpha$。
因为$\triangle CDF\backsim\triangle ABF$，$\frac{S_{\triangle CDF}}{S_{\triangle ABF}}=\left(\frac{CD}{AB}\right)^{2}$。
因为$\angle CAD=\angle CAF$（已证），$\angle ACD=\angle CAD$，$\angle ABC=\angle ACB$。
由$\triangle CDF\backsim\triangle ABF$，$\frac{S_{\triangle CDF}}{S_{\triangle ABF}}=\frac{1}{5}$。
综上，（1）已证$\triangle CDF\backsim\triangle ABF$；（2）①已证$\angle BAC = 2\angle CAF$；②$\frac{S_{\triangle CDF}}{S_{\triangle ABF}}=\frac{1}{5}$。