《2025年千里马单元测试卷八年级数学下册人教版》

1. 小华从老师提供的线段中选择三条首尾相连围成一个直角三角形，则他应该选择的三条线段的长度是 ( )
A.2,3,4
B.3,4,5
C.4,5,6
D.5,6,7

答案： B

2. 下列条件中不能判定△ABC是直角三角形的是 ( )
A. $AB^{2}+BC^{2}=AC^{2}$
B. $AB^{2}-BC^{2}=AC^{2}$
C. ∠A + ∠B = ∠C
D. ∠A:∠B:∠C = 3:4:5

答案： D

3. 命题“直角三角形两条直角边的平方和等于斜边的平方”的逆命题是____________________.

答案： 如果三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形

4. 如图,已知△ABC中,AB = 10,AC = 8,BC = 6,AB的垂直平分线分别交AC,AB于点D,E. 连接BD,则CD的长为_______.

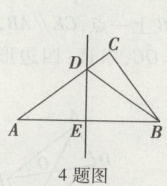
答案： $\frac{7}{4}$

5. 如图,点B为x轴上的一个动点,点A的坐标为(0,4),点C的坐标为(4,1),当点B的坐标为________时,△ABC为直角三角形.

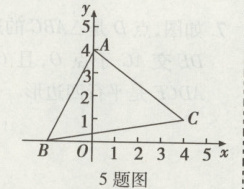
答案： $(\frac{13}{4},0)$或$(2,0)$或$(-3,0)$

6. 在平面直角坐标系中,△ABC的顶点坐标分别为A( - 2,0),B(8,0),C(0,4),证明:∠ACB = 90°.(写出必要的推理过程)

答案： 证明:$\because A(-2,0),B(8,0),C(0,4)$,
$\therefore AC^{2}=2^{2}+4^{2}=20,BC^{2}=8^{2}+4^{2}=80,AB^{2}=10^{2}=100$,
$\therefore AB^{2}=AC^{2}+BC^{2}$,
$\therefore \triangle ABC$是直角三角形,且$∠ACB = 90^{\circ}$.

7. 如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,道路AC因为施工需要封闭,该村为方便村民取水,决定在河边新建一个取水点H(A,H,B在同一条直线上),并新修一条道路CH,已知CB = $\sqrt{5}$千米,CH = 2千米,HB = 1千米.
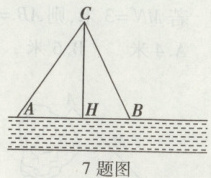
(1)CH是不是村庄C到河边最近的道路,请通过计算加以说明;
(2)已知新的取水点H与原取水点A相距1.5千米,求新路CH比原路CA少多少千米.

答案： 解:
(1)CH 是村庄 C 到河边最近的道路.
理由:$\because CH = 2$千米,$HB = 1$千米,$CB=\sqrt{5}$千米,
$\therefore CH^{2}+HB^{2}=CB^{2}$,
$\therefore \triangle BCH$为直角三角形,$∠BHC = 90^{\circ}$,$\therefore CH⊥AB$,
$\therefore CH$是村庄 C 到河边最近的道路.
(2)在$Rt\triangle ACH$中,$\because AH = 1.5$千米,$CH = 2$千米,
$\therefore AC=\sqrt{1.5^{2}+2^{2}}=2.5$(千米),
$\therefore AC - CH = 2.5 - 2 = 0.5$(千米),
∴ 新路 CH 比原路 CA 少 0.5 千米.