2025年千里马单元测试卷八年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年千里马单元测试卷八年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 如图,等边△ABC的边长是2,D,E分别为AB,AC的中点,连接CD,过点E作EF//CD交BC的延长线于点F.
(1)求证:DE = CF;
(2)求EF的长.

(1)求证:DE = CF;
(2)求EF的长.

答案:
(1)证明:
∵D,E分别为AB,AC的中点,
∴DE//BC,DE = $\frac{1}{2}$BC,即DE//CF.
∵EF//CD,
∴四边形DEFC是平行四边形,
∴DE = CF.
(2)解:
∵四边形DEFC是平行四边形,
∴DC = EF.
∵D为AB的中点,等边△ABC的边长是2,
∴AD = BD = 1,CD⊥AB,BC = 2,
∴EF = DC = $\sqrt{3}$.
(1)证明:
∵D,E分别为AB,AC的中点,
∴DE//BC,DE = $\frac{1}{2}$BC,即DE//CF.
∵EF//CD,
∴四边形DEFC是平行四边形,
∴DE = CF.
(2)解:
∵四边形DEFC是平行四边形,
∴DC = EF.
∵D为AB的中点,等边△ABC的边长是2,
∴AD = BD = 1,CD⊥AB,BC = 2,
∴EF = DC = $\sqrt{3}$.
9. (株洲中考)如图所示,在△ABC中,D,E分别为AB,AC的中点,点H在线段CE上,连接BH,G,F分别为BH,CH的中点.
(1)求证:四边形DEFG为平行四边形;
(2)DG⊥BH,BD = 3,EF = 2,求线段BG的长度.

(1)求证:四边形DEFG为平行四边形;
(2)DG⊥BH,BD = 3,EF = 2,求线段BG的长度.

答案:
(1)证明:
∵D,E分别为AB,AC的中点,G,F分别为BH,CH的中点,
∴DE是△ABC的中位线,GF是△HBC的中位线,
∴DE//BC,DE = $\frac{1}{2}$BC,GF//BC,GF = $\frac{1}{2}$BC,
∴DE//GF,DE = GF,
∴四边形DEFG为平行四边形.
(2)解:四边形DEFG为平行四边形,
∴DG = EF = 2.
∵DG⊥BH,
∴∠DGB = 90°,
∴BG = $\sqrt{BD^{2}-DG^{2}}$ = $\sqrt{3^{2}-2^{2}}$ = $\sqrt{5}$.
(1)证明:
∵D,E分别为AB,AC的中点,G,F分别为BH,CH的中点,
∴DE是△ABC的中位线,GF是△HBC的中位线,
∴DE//BC,DE = $\frac{1}{2}$BC,GF//BC,GF = $\frac{1}{2}$BC,
∴DE//GF,DE = GF,
∴四边形DEFG为平行四边形.
(2)解:四边形DEFG为平行四边形,
∴DG = EF = 2.
∵DG⊥BH,
∴∠DGB = 90°,
∴BG = $\sqrt{BD^{2}-DG^{2}}$ = $\sqrt{3^{2}-2^{2}}$ = $\sqrt{5}$.
10. 已知四边形ABCD为平行四边形,点M,N分别是直线AD,BC上的点,且与点A,B,C,D不重合.
(1)请在图①中画出你设计的图形,并添加一个适当的条件: ________,使得点M,N与□ABCD的两个顶点组成的四边形是一个平行四边形,并说明理由;
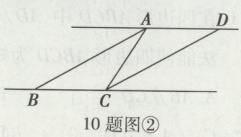
(2)如图②,已知AC = BC = 6,若∠ABC = 30°,四边形AMCN为平行四边形,且AM = 6,求MC的长度.
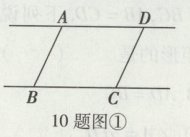
(1)请在图①中画出你设计的图形,并添加一个适当的条件: ________,使得点M,N与□ABCD的两个顶点组成的四边形是一个平行四边形,并说明理由;
(2)如图②,已知AC = BC = 6,若∠ABC = 30°,四边形AMCN为平行四边形,且AM = 6,求MC的长度.


答案:
解:
(1)设计图形如答图①(设计图形不唯一).
AM = CN(答案不唯一)
理由:
∵四边形ABCD是平行四边形,
∴AD = BC,AD//BC,
∴DM = BN,
∴四边形MBND是平行四边形.

(2)如答图②.
∵四边形ABCD是平行四边形,四边形AMCN为平行四边形,
∴AM//BN,
∴∠MAB = ∠ABC = 30°.
∵AC = BC = 6,
∴∠CAB = ∠CBA = 30°,
∴∠MAB = ∠CAB = 30°,
∴∠MAC = 60°.
∵AC = AM = 6,
∴△ACM是等边三角形,
∴MC = 6.

解:
(1)设计图形如答图①(设计图形不唯一).
AM = CN(答案不唯一)
理由:
∵四边形ABCD是平行四边形,
∴AD = BC,AD//BC,
∴DM = BN,
∴四边形MBND是平行四边形.

(2)如答图②.
∵四边形ABCD是平行四边形,四边形AMCN为平行四边形,
∴AM//BN,
∴∠MAB = ∠ABC = 30°.
∵AC = BC = 6,
∴∠CAB = ∠CBA = 30°,
∴∠MAB = ∠CAB = 30°,
∴∠MAC = 60°.
∵AC = AM = 6,
∴△ACM是等边三角形,
∴MC = 6.

查看更多完整答案,请扫码查看


