2025年千里马单元测试卷八年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年千里马单元测试卷八年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 以2,3为直角边长的直角三角形的斜边长为( )
A. $\sqrt{5}$
B. $\sqrt{13}$
C. 4
D. 5
A. $\sqrt{5}$
B. $\sqrt{13}$
C. 4
D. 5
答案:
B
2. 如图,所有阴影部分的四边形都是正方形,所有三角形都是直角三角形,已知正方形A,B,C的面积依次为2,4,3,则正方形D的面积为( )
A. 7 B. 8 C. 9 D. 10

A. 7 B. 8 C. 9 D. 10

答案:
C
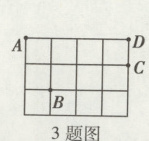
3. 如图,在4×3的正方形网格(每个小正方形的边长都是1)中,标记格点A,B,C,D,则下列线段长度为$\sqrt{10}$的是( )
A. 线段AB B. 线段BC
C. 线段AC D. 线段BD
A. 线段AB B. 线段BC
C. 线段AC D. 线段BD

答案:
B
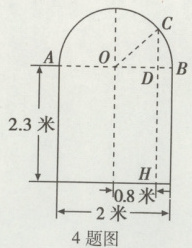
4. 一辆装满货物,宽为1.6米的卡车,欲通过如图所示的隧道($\overparen{AB}$为以AB为直径的半圆),则卡车的高度必须低于( )
A. 3.0米 B. 2.9米 C. 2.8米 D. 2.7米
A. 3.0米 B. 2.9米 C. 2.8米 D. 2.7米

答案:
B
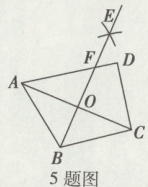
5. 如图,在四边形ABCD中,AD//BC,∠D = 90°,AD = 4,BC = 3,分别以点A,C为圆心,大于$\frac{1}{2}$AC长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O. 若点O是AC的中点,则CD的长为( )
A. $2\sqrt{2}$ B. 4 C. 3 D. $\sqrt{10}$
A. $2\sqrt{2}$ B. 4 C. 3 D. $\sqrt{10}$

答案:
A[解析]如答图,连接FC,则AF = FC.
∵AD//BC,
∴∠FAO = ∠BCO.
在△FOA与△BOC中,
$\left\{\begin{array}{l} \angle FAO=\angle BCO,\\ OA = OC,\\ \angle AOF=\angle COB,\end{array}\right.$
∴△FOA≌△BOC(ASA),
∴AF = BC = 3,
∴FC = AF = 3,FD = AD - AF = 4 - 3 = 1.
在Rt△FDC中,
∵∠D = 90°,
∴CD² + DF² = FC²,
∴CD² + 1² = 3²,
∴CD = $2\sqrt{2}$. 故选A.

A[解析]如答图,连接FC,则AF = FC.
∵AD//BC,
∴∠FAO = ∠BCO.
在△FOA与△BOC中,
$\left\{\begin{array}{l} \angle FAO=\angle BCO,\\ OA = OC,\\ \angle AOF=\angle COB,\end{array}\right.$
∴△FOA≌△BOC(ASA),
∴AF = BC = 3,
∴FC = AF = 3,FD = AD - AF = 4 - 3 = 1.
在Rt△FDC中,
∵∠D = 90°,
∴CD² + DF² = FC²,
∴CD² + 1² = 3²,
∴CD = $2\sqrt{2}$. 故选A.

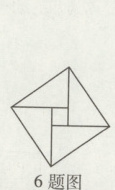
6. 我国古代数学家赵爽巧妙地用“弦图”证明了勾股定理,标志着中国古代的数学成就. 如图,弦图中四个全等的直角三角形的两条直角边长分别为3和4,则中间小正方形的对角线长为________.

答案:
$\sqrt{2}$
7. (东营中考)一艘船由A港沿北偏东60°方向航行30 km至B港,然后沿北偏西30°方向航行________ km至C港,则A,C两港之间的距离为________ km.
答案:
50 [解析]如答图.
由题意,得∠DAB = 60°,
∠FBC = 30°,AD//EF,
∴∠DAB = ∠ABE = 60°,
∴∠ABC = 180° - ∠ABE - ∠FBC = 90°.
在Rt△ABC中,AB = 30 km,BC = 40 km,
∴AC = $\sqrt{AB^{2}+BC^{2}}=\sqrt{30^{2}+40^{2}} = 50$(km).

50 [解析]如答图.
由题意,得∠DAB = 60°,
∠FBC = 30°,AD//EF,
∴∠DAB = ∠ABE = 60°,
∴∠ABC = 180° - ∠ABE - ∠FBC = 90°.
在Rt△ABC中,AB = 30 km,BC = 40 km,
∴AC = $\sqrt{AB^{2}+BC^{2}}=\sqrt{30^{2}+40^{2}} = 50$(km).

8. (哈尔滨南岗区期末)在△ABC中,∠ABC = 60°,AB = 8,AC = $2\sqrt{13}$,则BC的长为________.
答案:
6或2 [解析]过点A作AD⊥BC于点D,当点D在线段BC上时,如答图①.
∵∠ABC = 60°,∠ADB = 90°,
∴∠BAD = 30°,
∴BD = $\frac{1}{2}$AB = 4,
∴AD = $\sqrt{AB^{2}-BD^{2}}=\sqrt{8^{2}-4^{2}} = 4\sqrt{3}$. 在Rt△ACD中,由勾股定理,得CD = $\sqrt{AC^{2}-AD^{2}}=\sqrt{(2\sqrt{13})^{2}-(4\sqrt{3})^{2}} = 2$,
∴BC = BD + CD = 4 + 2 = 6. 当点D在线段BC的延长线上时,如答图②. 同理可得BC = BD - CD = 4 - 2 = 2.
∴BC = 6或2.

6或2 [解析]过点A作AD⊥BC于点D,当点D在线段BC上时,如答图①.
∵∠ABC = 60°,∠ADB = 90°,
∴∠BAD = 30°,
∴BD = $\frac{1}{2}$AB = 4,
∴AD = $\sqrt{AB^{2}-BD^{2}}=\sqrt{8^{2}-4^{2}} = 4\sqrt{3}$. 在Rt△ACD中,由勾股定理,得CD = $\sqrt{AC^{2}-AD^{2}}=\sqrt{(2\sqrt{13})^{2}-(4\sqrt{3})^{2}} = 2$,
∴BC = BD + CD = 4 + 2 = 6. 当点D在线段BC的延长线上时,如答图②. 同理可得BC = BD - CD = 4 - 2 = 2.
∴BC = 6或2.

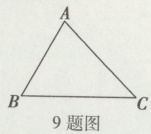
9. 如图,在△ABC中,∠B = 60°,∠C = 45°,BC = $6 + 6\sqrt{3}$. 求△ABC中BC边上的高.

答案:
解:如答图,过点A作AH⊥BC于点H.
在Rt△ABH中,∠B = 60°,则∠BAH = 30°,
∴AB = 2BH.
∵AB² = BH² + AH²,
∴(2BH)² = BH² + AH²,
∴BH = $\frac{\sqrt{3}}{3}$AH.
在Rt△AHC中,∠C = 45°,
∴CH = AH.
∵BC = 6 + 6$\sqrt{3}$,
∴$\frac{\sqrt{3}}{3}$AH + AH = 6 + 6$\sqrt{3}$,解得AH = 6$\sqrt{3}$.
故△ABC中BC边上的高是6$\sqrt{3}$.

解:如答图,过点A作AH⊥BC于点H.
在Rt△ABH中,∠B = 60°,则∠BAH = 30°,
∴AB = 2BH.
∵AB² = BH² + AH²,
∴(2BH)² = BH² + AH²,
∴BH = $\frac{\sqrt{3}}{3}$AH.
在Rt△AHC中,∠C = 45°,
∴CH = AH.
∵BC = 6 + 6$\sqrt{3}$,
∴$\frac{\sqrt{3}}{3}$AH + AH = 6 + 6$\sqrt{3}$,解得AH = 6$\sqrt{3}$.
故△ABC中BC边上的高是6$\sqrt{3}$.

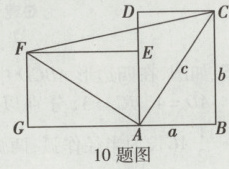
10. 一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法. 如图,火柴盒的一个侧面ABCD(是长方形)倒下到AEFG的位置,连接CF,此时∠FAC = 90°,AB = a,BC = b,AC = c. 请利用直角梯形BCFG的面积证明勾股定理:$a^{2}+b^{2}=c^{2}$.

答案:
证明:
∵$S_{梯形BCFG}=S_{\triangle AFG}+S_{\triangle ACB}+S_{\triangle AFC}=\frac{1}{2}ab+\frac{1}{2}ab+\frac{1}{2}c^{2}=ab+\frac{1}{2}c^{2}$,
$S_{梯形BCFG}=\frac{1}{2}\cdot (FG + BC)\cdot BG=\frac{1}{2}(a + b)(a + b)=\frac{1}{2}a^{2}+ab+\frac{1}{2}b^{2}$,
∴$ab+\frac{1}{2}c^{2}=\frac{1}{2}a^{2}+ab+\frac{1}{2}b^{2}$,
整理,得$a^{2}+b^{2}=c^{2}$.
∵$S_{梯形BCFG}=S_{\triangle AFG}+S_{\triangle ACB}+S_{\triangle AFC}=\frac{1}{2}ab+\frac{1}{2}ab+\frac{1}{2}c^{2}=ab+\frac{1}{2}c^{2}$,
$S_{梯形BCFG}=\frac{1}{2}\cdot (FG + BC)\cdot BG=\frac{1}{2}(a + b)(a + b)=\frac{1}{2}a^{2}+ab+\frac{1}{2}b^{2}$,
∴$ab+\frac{1}{2}c^{2}=\frac{1}{2}a^{2}+ab+\frac{1}{2}b^{2}$,
整理,得$a^{2}+b^{2}=c^{2}$.
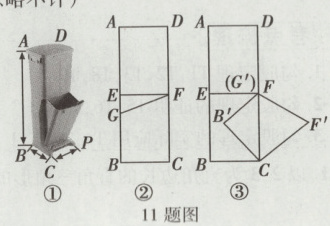
11. 新情境如图①,某厂家设计了一种双层长方体垃圾桶,AB = 84 cm,BC = 30 cm,CP = 36 cm,侧面示意图如图②所示,EF为隔板,等分上、下两层. 将下方内桶BCFG绕底部轴(CP)旋转打开后,内桶刚好卡在隔板边沿,侧面示意图如图③所示,求BG的长度. (板材厚度忽略不计)

答案:
解:如答图,连接CG,过点G作GT⊥CF于点T,易知四边形BCTG是长方形,
∴BG = CT,GT = BC = 30 cm,
易知CF = CG = $\frac{1}{2}$CD = $\frac{1}{2}$AB = 42(cm),
∴BG = CT = $\sqrt{CG^{2}-GT^{2}}=\sqrt{42^{2}-30^{2}} = 12\sqrt{6}$(cm).

解:如答图,连接CG,过点G作GT⊥CF于点T,易知四边形BCTG是长方形,
∴BG = CT,GT = BC = 30 cm,
易知CF = CG = $\frac{1}{2}$CD = $\frac{1}{2}$AB = 42(cm),
∴BG = CT = $\sqrt{CG^{2}-GT^{2}}=\sqrt{42^{2}-30^{2}} = 12\sqrt{6}$(cm).

查看更多完整答案,请扫码查看


