《2025年千里马单元测试卷八年级数学下册人教版》

1.（山西中考）一种弹簧秤能称不超过10 kg的物体，不挂物体时弹簧的长度为12 cm，每挂质量为1 kg的物体，弹簧伸长0.5 cm. 在弹性限度内，挂重后弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数关系式为（ ）

A. y = 12 - 0.5x
B. y = 12 + 0.5x
C. y = 10 + 0.5x
D. y = 0.5x

答案： B

2. 在测量液体密度的实验中，小华同学测得液体和烧杯的总质量与液体体积的关系如图所示，则下列选项中不正确的是（ ）

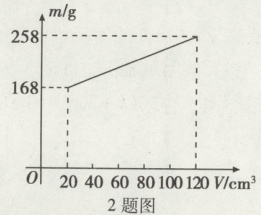
A. 空烧杯的质量是168 g
B. 液体的质量与液体的体积满足一次函数关系
C. 液体的密度是900 kg/m³
D. 当液体体积为60 cm³时，液体和烧杯的总质量为204 g

答案： A [解析]设m与V的函数关系式为m = kV + b(k≠0),根据题图可知$\begin{cases}20k + b = 168 \\120k + b = 258 \end{cases}$,解得$\begin{cases}k = 0.9 \\b = 150 \end{cases}$,$\therefore$m = 0.9V + 150.当V = 0时,m = 150,即空烧杯的质量是150g,故选项A符合题意;函数图象是一条线段,则液体与烧杯的总质量与液体体积满足一次函数关系，因为烧杯的质量是一定的，所以液体的质量与液体的体积满足一次函数关系，故选项B不符合题意;由液体的密度=$\frac{液体的质量}{液体的体积}$知，液体的密度为$\frac{258 - 168}{120 - 20}$ = 0.9g/cm³ = 900kg/m³,故选项C不符合题意;把V = 60代入m = 0.9V + 150,得m = 204,$\therefore$当液体体积为60cm³时,液体和烧杯的总质量为204g,故选项D不符合题意.故选A.

3. 甲、乙两个工程队同时修建两条长为1 000米的马路，所修建的马路的长度y(米)与天数x(天)之间的函数关系如图所示，下列说法不正确的是（ ）

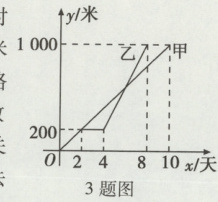
A. 甲工程队每天修建100米
B. 甲、乙两工程队6天修建的马路长度相同
C. 乙工程队休息前修建的速度比休息后修建的速度每天慢40米
D. 乙工程队比甲工程队早2天完成任务

答案： C

4. 某市出租车白天的收费起步价为14元，即路程不超过3千米时收费14元，超过部分每千米收费2.4元，若乘客白天乘坐出租车的路程为x(x ＞ 3)千米，乘车费为y元，则y与x之间的关系式为______________.

答案： y = 2.4x + 6.8

5. 甲、乙两工程队完成某项工程，甲先做了10天，然后乙加入合作，共同完成剩下的工程. 设工程总量为1，若工程进度如图所示，则实际完成这项工程共需要______________天.

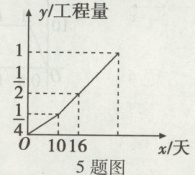
答案： 28

6. 某班52名师生准备去亮子河旅游，为确定旅游费用，班主任刘老师派班长去了解船只租金情况，班长得到如下表格：
(1)如果两种船都租，且既不超载也不空载，那么你能设计出几种租船方案？
(2)若你是班长，为了使总租金最少，应该选择怎样的租船方案？

答案： 解:
(1)设租A型船x只,B型船y只,可得5x + 3y = 52(x,y取正整数),
解得$\begin{cases}x = 2 \\y = 14 \end{cases}$或$\begin{cases}x = 5 \\y = 9 \end{cases}$或$\begin{cases}x = 8 \\y = 4 \end{cases}$,
即如果两种船都租,且既不超载也不空载,一共有三种设计方案:
方案一,租用A型船2只,B型船14只;
方案二,租用A型船5只,B型船9只;
方案三,租用A型船8只,B型船4只.
(2)方案一的租金为160×2 + 105×14 = 1790(元),
方案二的租金为160×5 + 105×9 = 1745(元),
方案三的租金为160×8 + 105×4 = 1700(元).
由上可得方案三租金最少,
故使总租金最少,应该选择的租船方案是A型船8只,B型船4只.