《2025年53精准练九年级数学下册华师大版山西专版》

11. 已知$A(-1, y_{1})$、$B(-3, y_{2})$、$C(2, y_{3})$是抛物线$y = mx^{2}(m＜0)$上的三个点，比较$y_{1}$、$y_{2}$、$y_{3}$的大小，正确的是（ ）
A. $y_{1}＞y_{2}＞y_{3}$
B. $y_{1}＜y_{2}＜y_{3}$
C. $y_{3}＞y_{1}＞y_{2}$
D. $y_{1}＞y_{3}＞y_{2}$

答案： D

12. [2024呼和浩特二模改编]下列图象中，当$ab＞0$时，函数$y = ax^{2}$与$y = ax + b$的图象可能是（ ）

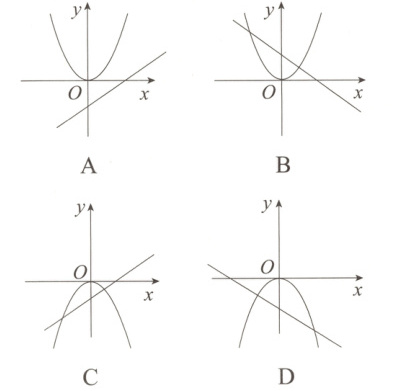
答案： D

13. 如图，①$y = ax^{2}$；②$y = bx^{2}$；③$y = cx^{2}$；④$y = dx^{2}$.比较$a$，$b$，$c$，$d$的大小：____________________.（用“＞”连接）
　　　　　　

答案： $a＞b＞d＞c$

14. [转化思想]如图，正方形的边长为4，以正方形中心为原点建立平面直角坐标系，作出函数$y = 2x^{2}$与$y = -2x^{2}$的图象，则阴影部分的面积是________.
　　　　　　

答案： 8

15. 如图，正方形的四个顶点的坐标依次是$(1, 1)$、$(3, 1)$、$(3, 3)$、$(1, 3)$，若抛物线$y = ax^{2}$与正方形有交点，则实数$a$的取值范围是____________.
　　　　　

答案： $\frac{1}{9}\leq a\leq3$

16. [分类讨论]已知抛物线$y=\frac{4}{9}x^{2}$与直线$y = x + m$都经过点$A(3, n)$.
(1)求$m$、$n$的值.
(2)在$x$轴上是否存在点$P$，使得$\triangle AOP$是等腰三角形？若存在，请求出点$P$的坐标；若不存在，请说明理由.
　　　　　　　　　

答案： 解：
(1)把$A(3,n)$代入$y = \frac{4}{9}x^{2}$，得
$n=\frac{4}{9}\times3^{2}=4$，
$\therefore A(3,4)$，
把$A(3,4)$代入$y = x + m$，得$m = 1$．
(2)存在．
由
(1)得$OA=\sqrt{3^{2}+4^{2}} = 5$．
分三种情况：
①当$OP = OA$时，易得$P_{1}(5,0)$，$P_{2}(-5,0)$．
②当$AP = AO$时，根据三线合一可知$P_{3}(6,0)$．
③当$PA = PO$时，设$P(a,0)$，
则$PA^{2}=(a - 3)^{2}+16$，$OP^{2}=a^{2}$，
$\therefore(a - 3)^{2}+16=a^{2}$，
解得$a=\frac{25}{6}$，
$\therefore P_{4}(\frac{25}{6},0)$．
综上所述，点$P$的坐标为$(5,0)$或$(-5,0)$或$(6,0)$或$(\frac{25}{6},0)$．