《2025年53精准练九年级数学下册华师大版山西专版》

4. 已知点$A(1,y_{1})$，$B(2,y_{2})$在抛物线$y=-(x + 1)^{2}+2$上，则下列结论正确的是（ ）
A. $2＞y_{1}＞y_{2}$
B. $2＞y_{2}＞y_{1}$
C. $y_{1}＞y_{2}＞2$
D. $y_{2}＞y_{1}＞2$

答案： A

5. 抛物线$C_{1}$：$y = 2(x - 3)^{2}+1$与抛物线$C_{2}$：$y=a(x - h)^{2}+k$关于$x$轴对称，则抛物线$C_{2}$所对应的函数表达式是（ ）
A. $y=-2(x - 3)^{2}-1$
B. $y = 2(x + 3)^{2}+1$
C. $y=-2(x + 3)^{2}-1$
D. $y=-2(x - 3)^{2}+1$

答案： A

6. 某广场有一喷水池，水从地面喷出，如图，以出水点为原点建立平面直角坐标系，水在空中的轨迹是抛物线$y=-x^{2}+6x$的一部分，则水喷出的最大高度是________米.

答案： 9

7. [2024温州期中]如图，将某运动员所扔铅球的运动轨迹看成抛物线的一部分，铅球达到的高度$y$(m)与行进水平距离$x$(m)之间的关系式为$y = -\frac{1}{8}x^{2}+\frac{15}{8}x + 2$，则此次的成绩为（ ）

A. $4$ m
B. $8$ m
C. $12$ m
D. $16$ m

答案： D

8. 如图，抛物线$y = ax^{2}+bx + c$（$a\neq0$）的对称轴为直线$x = -3$，$(-1,-4)$是抛物线上的点，结合图象给出如下结论：①$abc＜0$；②$b^{2}＞4ac$；③$a - b + c = 0$；④当$x = -3$时，$y$有最小值.其中正确的结论是（ ）

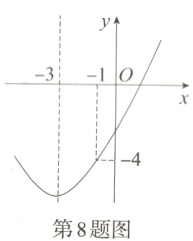
A. ①②③
B. ①②④
C. ②③④
D. ①②③④

答案： B

9. 如图，抛物线$y = ax^{2}+c$与直线$y = mx + n$交于$A(-1,p)$，$B(3,q)$两点，则当$ax^{2}-mx + c＞n$时，$x$的取值范围是________.

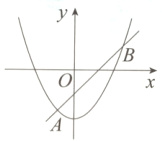
答案： $x ＜ -1$或$x ＞ 3$

10. [2023忻州静乐县期末]如图，抛物线形拱桥的拱顶离水面2米时，水面宽4米，若水面下降2.5米，则水面宽度为（ ）

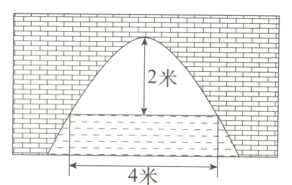
A. 3米
B. 6米
C. 8米
D. 9米

答案： B

11. [2023晋城一中期中]直播带货已经成为一种流行的销售方式，某主播在直播间销售一种成本为每件100元的手工艺品，若按每件150元销售，一天可售出40件.为了减少库存，该主播决定降价销售，每件的售价每降低1元，每天的销量就增加2件，设该手工艺品的售价为每件$x$元（$x\geq100$），每天的销售利润为$w$元.
(1)写出$w$关于$x$的函数关系式.
(2)当售价定为每件多少元时，才能使每天获得的利润最大？并求出最大利润.

答案： 解：
(1)$w=(x - 100)[40 + 2(150 - x)]$，
整理得$w=-2x^{2}+540x - 34000$。
(2)由
(1)得$w=-2(x - 135)^{2}+2450$，
$\because -2 ＜ 0$，
$\therefore$当$x = 135$时，$w$最大，最大值为2450。
答：当售价定为每件135元时，才能使每天获得的利润最大，最大利润为2450元。