《2025年53精准练九年级数学下册华师大版山西专版》

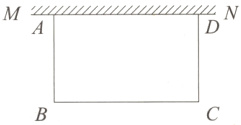
6. [2024深圳期中]如图，在一块空地上有一段长为10 m的旧墙MN，王大爷利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了24 m木栏.则矩形菜园ABCD面积的最大值为 （ ）

A. 72 m²
B. 70 m²
C. 144 m²
D. 140 m²

答案： B

7. 如图，矩形ABCD中，AB = 2 cm，AD = 5 cm，动点P从点A出发，以1 cm/s的速度沿AD向终点D移动，设移动时间为t s.连结PC，以PC为一边作正方形PCEF，连结DE、DF，则△DEF面积的最小值为 （ ）

A. $\frac{3}{2}$ cm²
B. $\frac{3}{4}$ cm²
C. $\frac{4}{5}$ cm²
D. $\frac{8}{5}$ cm²

答案： A
详解：$\because$四边形$PCEF$是正方形，
$\therefore S_{\triangle PCD}+S_{\triangle DEF}=\frac{1}{2}S_{正方形PCEF}$，
由题意得$PD=(5 - t)\text{cm}$，$CD = AB = 2\text{cm}$，
$\therefore S_{\triangle PCD}=\frac{1}{2}\times2(5 - t)=(5 - t)\text{cm}^{2}$.
在$Rt\triangle PCD$中，$PC^{2}=PD^{2}+CD^{2}=(5 - t)^{2}+4=t^{2}-10t + 29$，
$\therefore S_{\triangle DEF}=\frac{1}{2}(t^{2}-10t + 29)-(5 - t)=\frac{1}{2}t^{2}-4t+\frac{19}{2}=\frac{1}{2}(t - 4)^{2}+\frac{3}{2}$，
$\because \frac{1}{2}＞0$，
$\therefore$当$t = 4$时，$S_{\triangle DEF}$最小，为$\frac{3}{2}\text{cm}^{2}$.

8. [2023昆明期中]在边长为6 cm的正方形ABCD中，点E、F、G、H分别按A→B、B→C、C→D、D→A的方向同时出发，均以1 cm/s的速度匀速运动.写出四边形EFGH的面积S(cm²)关于运动时间t(s)的函数关系式，当运动几秒时，四边形EFGH的面积最小？最小面积是多少？

答案： 解：由题意得$AE = t\text{cm}$，
$EB=(6 - t)\text{cm}$，
则$S = 6^{2}-\frac{1}{2}t\cdot(6 - t)\cdot4=2(t - 3)^{2}+18$，
$\because 2＞0$，
$\therefore$当$t = 3$时，$S$取最小值，为18.
答：当运动3 s时，四边形$EFGH$的面积最小，最小面积是18$\text{cm}^{2}$.

9. 如图，四边形ABCD是一块边长为4米的正方形苗圃，园林部门拟将其改造为矩形AEFG的形状，点E在AB边上，点G在AD的延长线上，DG = 2BE，设BE的长为x米，改造后矩形苗圃AEFG的面积为y平方米.
(1)y与x之间的函数关系式为________________(不需写自变量的取值范围).
(2)根据改造方案改造后的矩形苗圃AEFG的面积与原正方形苗圃ABCD的面积相等，请问此时BE的长为多少米？
(3)当BE的长为多少米时，改造后的矩形苗圃AEFG的面积最大？并求出最大面积.

答案： 解：
(1)$y=-2x^{2}+4x + 16$.
(2)根据题意可得$-2x^{2}+4x + 16 = 16$，解得$x_{1}=2$，$x_{2}=0$(舍去).
答：$BE$的长为2米.
(3)$y=-2x^{2}+4x + 16=-2(x - 1)^{2}+18$，
$\because -2＜0$，
$\therefore$当$x = 1$时，$y$取最大值，为18.
答：当$BE$的长为1米时，改造后的矩形苗圃$AEFG$的面积最大，最大面积为18平方米.