《2025年学习探究诊断高中数学选择性必修第一册》

一、选择题

答案：

1. 已知空间向量$\boldsymbol{a}=(2,3,1),\boldsymbol{b}=(1,2,0)$，则$|\boldsymbol{a}+\boldsymbol{b}|$等于( )
（A）$\sqrt{3}$ （B）$\sqrt{35}$ （C）3 （D）9

答案： B

2. 设空间向量$\boldsymbol{a}=(x,-1,3),\boldsymbol{b}=(2,y,6)$，且$\boldsymbol{a}//\boldsymbol{b}$，则( )
（A）$x = 1,y = - 2$ （B）$x = 1,y = 2$ （C）$x=\frac{1}{2},y = - 2$ （D）$x = - 1,y = - 2$

答案： A

3. 正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，下列各式中运算结果为向量$\overrightarrow{B_{1}D_{1}}$的是( )
①$\overrightarrow{A_{1}D_{1}}-\overrightarrow{A_{1}A}-\overrightarrow{AB}$；②$\overrightarrow{BC}+\overrightarrow{BB_{1}}-\overrightarrow{D_{1}C_{1}}$；③$\overrightarrow{AD}-\overrightarrow{AB_{1}}+\overrightarrow{DD_{1}}$；④$\overrightarrow{B_{1}D_{1}}-\overrightarrow{AA_{1}}+\overrightarrow{DD_{1}}$.
（A）①② （B）②③ （C）③④ （D）①④

答案： C

4. 若$O,A,B,C$为空间中的四个点，则一定能使$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$为空间的一个基底的条件是( )
（A）$O,A,B,C$四点共面，但不共线 （B）$O,A,B,C$四点不共线
（C）$O,A,B,C$四点中任意三点不共线 （D）$O,A,B,C$四点不共面

答案： D

5. 如图，在正四棱柱$ABCD - A_{1}B_{1}C_{1}D_{1}$中，$AA_{1}=2AB$，则异面直线$A_{1}B$与$AD_{1}$所成角的余弦值为( )
（A）$\frac{1}{5}$ （B）$\frac{2}{5}$ （C）$\frac{3}{5}$ （D）$\frac{4}{5}$

答案： D

二、填空题

答案：

6. 在空间直角坐标系$Oxyz$中，平面$\alpha$的一个法向量是$\boldsymbol{n}=(1,-1,2)$，且平面$\alpha$过点$A(0,3,1)$.若$P(x,y,z)$是平面$\alpha$上任意一点，则点$P$的坐标满足的方程是____________________.

答案： $x - y + 2z + 1 = 0$

7. 在四面体$O - ABC$中，$\overrightarrow{OA}=\boldsymbol{a},\overrightarrow{OB}=\boldsymbol{b},\overrightarrow{OC}=\boldsymbol{c}$，$D$为$BC$的中点，$E$为$AD$的中点，则$\overrightarrow{OE}=$__________（用$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$表示）.

答案： $\frac{1}{2}\boldsymbol{a}+\frac{1}{4}\boldsymbol{b}+\frac{1}{4}\boldsymbol{c}$

8. 如图，在长方体$ABCD - A_{1}B_{1}C_{1}D$中，$ABCD$是边长为1的正方形，$D_{1}B$与平面$ABCD$所成的角为$45^{\circ}$，则棱$AA_{1}$的长为________；二面角$B - DD_{1}-C$的大小为________.

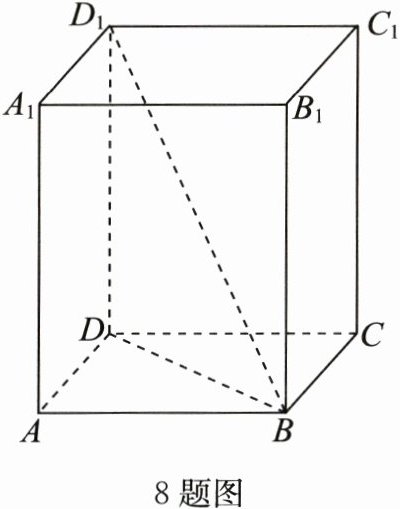
答案： $\sqrt{2},45^{\circ}$

9. 如图，在长方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，设$AD = AA_{1}=1,AB = 2$，则$|\overrightarrow{CC_{1}}-\overrightarrow{BD_{1}}|=$__________，$\overrightarrow{CC_{1}}\cdot\overrightarrow{CA_{1}}=$__________.

答案： $\sqrt{5},1$