《2025年学习探究诊断高中数学选择性必修第一册》

6. 设点$A(3,3,1),B(1,0,5),C(0,1,0)$，则$AB$的中点$M$到点$C$的距离$|CM| =$________.

答案： $\frac{\sqrt{53}}{2}$

7. 如图，在三棱锥$A - BCD$中，$DA,DB,DC$两两垂直，且$DB = DC$，$E$为$BC$的中点，则$\overrightarrow{AE}\cdot\overrightarrow{BC}$等于________.

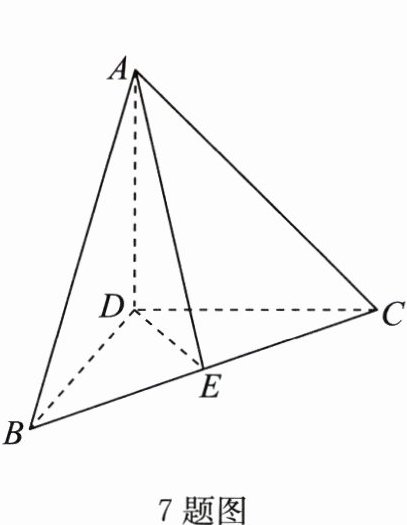
答案： 0

8. 已知空间向量$\boldsymbol{a}=(-1,1,-2),\boldsymbol{b}=(1,-2,-1),\boldsymbol{n}=(x,y,-2)$，其中$x,y\in\mathbf{R}$. 若$\boldsymbol{n}//\boldsymbol{b}$，则$\boldsymbol{a}\cdot\boldsymbol{n}=$__________.

答案： -2

9. 如图，在正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，直线$BC_{1}$和$B_{1}D_{1}$所成角的大小为________；直线$BC_{1}$和平面$B_{1}D_{1}DB$所成角的大小为________.

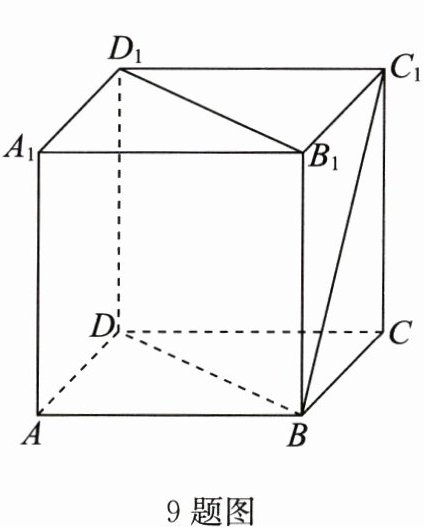
答案： $60^{\circ},30^{\circ}$

10. 如图，已知空间四边形$OABC$，$M,N$分别是对边$OA,BC$的中点，点$G$在线段$MN$上，且$MG = 2GN$，则用向量$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$表示，向量$\overrightarrow{OG}$为________________.

答案： $\frac{1}{6}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$

11. 如图，在正四棱柱$ABCD - A_{1}B_{1}C_{1}D_{1}$中，$AB = 4,AA_{1} = 8$，$E$为$CC_{1}$的中点，$O_{1}$为下底面正方形的中心.
（1）求异面直线$AB$与$EO_{1}$所成角的余弦值；
（2）求二面角$C - AB - O_{1}$的余弦值.

答案： 解：如图，建立空间直角坐标系$D_1xyz$， 则$A(4,0,8),B(4,4,8),O_1(2,2,0),E(0,4,4)$。
(1)$\overrightarrow{AB}=(0,4,0),\overrightarrow{EO_1}=(2,-2,-4)$， $|\cos\langle\overrightarrow{AB},\overrightarrow{EO_1}\rangle|=\frac{|\overrightarrow{AB}\cdot\overrightarrow{EO_1}|}{|\overrightarrow{AB}||\overrightarrow{EO_1}|}=\frac{\sqrt{6}}{6}$， 所以异面直线$AB$与$EO_1$所成角的余弦值为$\frac{\sqrt{6}}{6}$。
(2)$DD_1\perp$平面$ABC$，所以平面$ABC$的一个法向量为$\overrightarrow{D_1D}=(0,0,8)$， 设平面$ABO_1$的一个法向量为$\boldsymbol{m}=(x,y,z)$， $\overrightarrow{AB}=(0,4,0),\overrightarrow{AO_1}=(-2,2,-8)$， $\begin{cases}4y = 0\\-2x + 2y - 8z = 0\end{cases}$，所以$y = 0$，令$z = 1$，则$x = -4$，所以$\boldsymbol{m}=(-4,0,1)$。 则$\cos\langle\overrightarrow{D_1D},\boldsymbol{m}\rangle=\frac{\sqrt{17}}{17}$， 因为二面角$C - AB - O_1$为锐二面角，所以余弦值为$\frac{\sqrt{17}}{17}$。