《2024年练习部分九年级数学上册沪教版54制》

1. 已知Rt△ABC中,$\angle C= 90^\circ$,$\tan A= \frac{4}{3}$。你能否求出$\sin A和\cos B$的值？

答案： $解：因为在 Rt△ABC中，tanA=\frac {4}{3}$
$所以设BC=4x，AC=3x$
$所以AB=\sqrt{AC²+BC²}=5x$
$sinA=\frac {BC}{AB}=\frac {4x}{5x}=\frac {4}{5}$
$cosB=\frac {BC}{AB}=\frac {4x}{5x}=\frac {4}{5}$

2. 如图,图中提供了一种求$\tan 15^\circ$的方法。阅读并填空：
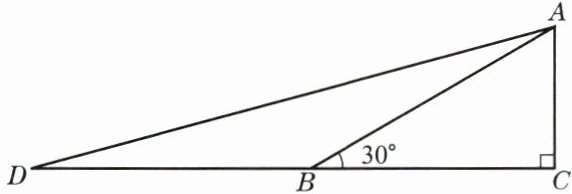
先作Rt△ABC,其中$\angle C= 90^\circ$,$\angle ABC= 30^\circ$；然后延长CB到点D,使$BD= AB$,联结AD。
(1)$\angle D= $______。
(2)设$AC= t$,那么$BC= $______(用t的代数式表示,以下同),$BD= $______。
(3)$\tan 15^\circ=$______。

答案： $15°$
$\sqrt{3}t$
$2t$
$2-\sqrt{3}$

3. 如图,在Rt△ABC中,$\angle C= 90^\circ$,$\angle ABC= 30^\circ$,BD是△ABC的角平分线,求$\tan 15^\circ$的值。(提示：过点D作$DE \perp AB$,垂足为点E。)

答案：
$解：设AC=a，$
$在Rt△ABC中，∠C=90°，∠ABC=30°，$
$∵tan∠ABC=\frac {AC}{BC}，$
$∴BC=\frac {a}{tan{30}°}=\sqrt{3}a.$
$过点D作DE⊥AB．垂足为点E，如图，$

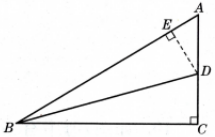
$∵BD是△ABC角平分线，$
$∴DE=DC，∠DBC=15°.$
$设CD=x，则DE=x，AD=a-x，$
$在Rt△ADE，∵sinA=\frac {DE}{AD}=sin{60}°=\frac {\sqrt{3}}{2}，$
$∴DE=\frac {\sqrt{3}}{2}AD，即x=\frac {\sqrt{3}}{2}(a-x)，$
$∴x=\frac {\sqrt{3}a}{2+\sqrt{3}}，$
$在Rt△BDC中，tan∠DBC=\frac {DC}{BC}=\frac {\frac {\sqrt{3}a}{2+\sqrt{3}}}{\sqrt{3}a}=\frac {1}{2+\sqrt{3}}=2-\sqrt{3}，$
$即tan{15}°=2-\sqrt{3}．$