(1)已知点 P 是线段 AB 上的黄金分割点,AP>PB,AB= 4 厘米,那么线段 AP、PB 的长分别是______厘米和______厘米.
(2)已知点 P 是线段 AB 上的黄金分割点,被分得的较长的线段 PB= 4 厘米,那么较短的线段 PA= ______厘米,AB= ______厘米.
(2)已知点 P 是线段 AB 上的黄金分割点,被分得的较长的线段 PB= 4 厘米,那么较短的线段 PA= ______厘米,AB= ______厘米.
答案:
$ 2\sqrt{5}-2$
$ 6-2\sqrt{5}$
$ 2\sqrt{5}-2$
$ 2\sqrt{5}+2$
$ 6-2\sqrt{5}$
$ 2\sqrt{5}-2$
$ 2\sqrt{5}+2$
2. 已知:如图,四边形 ABCD 的对角线 AC 与 BD 相交于点 O.
求证:$\frac{S_{\triangle AOB}}{S_{\triangle AOD}}= \frac{S_{\triangle COB}}{S_{\triangle COD}}$.
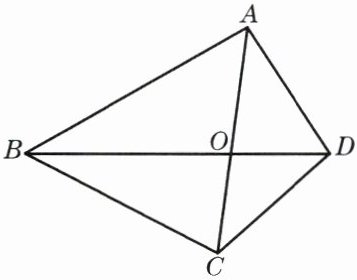
求证:$\frac{S_{\triangle AOB}}{S_{\triangle AOD}}= \frac{S_{\triangle COB}}{S_{\triangle COD}}$.

答案:
$ $
$证明:做AE⊥BD于点E$
$ ∵S_{△AOB}=\frac {1}{2}BO·AE,S_{△AOD}=\frac {1}{2}DO·AE,$
$ ∴\frac {{S}_{△AOB}}{{S}_{△AOD}}=\frac {BO}{DO},$
$ 同理可证\frac {{S}_{△COB}}{{S}_{△COD}}=\frac {BO}{DO},$
$ ∴\frac {{S}_{△AOB}}{{S}_{△AOD}}=\frac {{S}_{△COB}}{{S}_{△COD}}.$
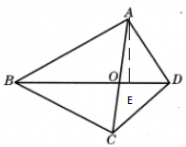
$ $
$证明:做AE⊥BD于点E$
$ ∵S_{△AOB}=\frac {1}{2}BO·AE,S_{△AOD}=\frac {1}{2}DO·AE,$
$ ∴\frac {{S}_{△AOB}}{{S}_{△AOD}}=\frac {BO}{DO},$
$ 同理可证\frac {{S}_{△COB}}{{S}_{△COD}}=\frac {BO}{DO},$
$ ∴\frac {{S}_{△AOB}}{{S}_{△AOD}}=\frac {{S}_{△COB}}{{S}_{△COD}}.$

3. 如图,已知梯形 ABCD 中,AB//DC,△AOB 的面积等于 9 平方厘米,△AOD 的面积等于 6 平方厘米.
(1)求△BOC 的面积.
(2)求$\frac{DO}{OB}和\frac{CO}{OA}$的值.

(1)求△BOC 的面积.
(2)求$\frac{DO}{OB}和\frac{CO}{OA}$的值.

答案:
$ 解:(1)∵△AOB的面积等于9平方厘米,△AOD的面积等于6平方厘米.$
$ ∴\frac {OD}{OB}=\frac {{S}_{△AOD}}{{S}_{△AOB}}=\frac {6}{9}=\frac {2}{3},$
$ ∵AB//DC,$
$ ∴△COD∽△ABO,$
$ ∴\frac {OC}{OA}=\frac {OD}{OB}=\frac {2}{3},$
$ ∴\frac {{S}_{△BOC}}{{S}_{△AOB}}=\frac {OC}{OA}=\frac {2}{3},$
$ ∴△BOC的面积=6平方厘米.$
$ (2)由(1)证得\frac {DO}{OB}=\frac {CO}{OA}=\frac {2}{3},$
$ ∴\frac {DO}{OB}和\frac {CO}{OA}的值都为\frac {2}{3}.$
$ ∴\frac {OD}{OB}=\frac {{S}_{△AOD}}{{S}_{△AOB}}=\frac {6}{9}=\frac {2}{3},$
$ ∵AB//DC,$
$ ∴△COD∽△ABO,$
$ ∴\frac {OC}{OA}=\frac {OD}{OB}=\frac {2}{3},$
$ ∴\frac {{S}_{△BOC}}{{S}_{△AOB}}=\frac {OC}{OA}=\frac {2}{3},$
$ ∴△BOC的面积=6平方厘米.$
$ (2)由(1)证得\frac {DO}{OB}=\frac {CO}{OA}=\frac {2}{3},$
$ ∴\frac {DO}{OB}和\frac {CO}{OA}的值都为\frac {2}{3}.$
查看更多完整答案,请扫码查看


