20.(本题满分14分)
设函数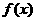 定义域为R,对任意实数x,y,有
定义域为R,对任意实数x,y,有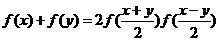 ,且
,且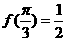 ,
,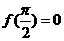 .
.
(1)求f(0)
(2)求证: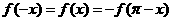 ;
;
(3)求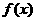 的周期;
的周期;
(4)(理科)若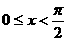 时,
时,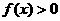 ,求证:
,求证: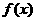 在
在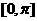 上单调递减.
上单调递减.
2005年高中数学调研卷(12月) 答卷
答卷
19.(本小题满分14分)
设双曲线 的两个焦点分别为F1、F2,离心率为2.
(1)若A、B分别为此双曲线的渐近线l1、l2上的动点,且2|AB|=5| F1F2|,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线;
(2)过点N(1, 0)能否作出直线l,使l交双曲线于P、Q两点,且→OP∙→OQ =0,若存在,求出直线l的方程;若不存在,说明理由.
18.(本小题满分14分)
(理科)已知数列{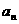 }中,
}中,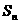 是其前n项和,且
是其前n项和,且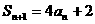 ,
,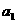 =1
=1
(1)若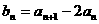 (
( ), 求证{
), 求证{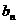 }为等比数列;
}为等比数列;
(2)若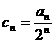 (
( ),求证{
),求证{ }为等差数列;
}为等差数列;
(3)求数列{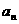 }的通项
}的通项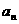 .
.
(文科)已知等差数列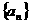 中,
中,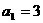 ,前n项和
,前n项和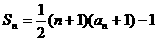 .
.
(1)求数列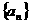 的公差d;
的公差d;
(2)记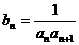 ,求数列
,求数列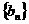 的前n项和为
的前n项和为 ;
;
(3)在(2)条件下,是否存在实数M,使得 ≤
≤ 对一切正整数n都成立?若存在,求出M的最小值.
对一切正整数n都成立?若存在,求出M的最小值.
17.(本小题满分14分)在一段笔直的古运河上建有5座拱桥An(n=1,2,3,4,5),经测量知,相邻两座桥之间的距离|AnAn+1|近似满足| AnAn+1|=800+150n(n = 1,2,3,4)米,某公司在每座桥边建有一个货物仓库Bn(n=1,2,3,4,5),其中B1仓库存有货物10吨,B2仓库存有货物20吨,B5仓库存有货物40吨,其他仓库是空的,现在河道上选择一点集中这些仓库的货物,以便于公司对外运输,如果每吨货物水上运输1千米需要0.5元运输费,那么选择哪一点使这批货物的运费最省?
16.(本小题满分14分)
已知A,B,D三点不在同一条直线上,且A(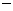 2,0),B(2,0),
2,0),B(2,0),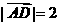 ,
,
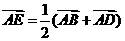 .
.
(1)求点E的轨迹方程;
(2)设过点A的直线l与E点的轨迹相切,与以A,B为焦点的椭圆F相交于M,N两点,且线段MN的中点到y轴的距离为 。求此椭圆F的方程.
。求此椭圆F的方程.
13.(文科)设e1,e2分别为双曲线和它的共轭双曲线的离心率,给出下列结论:
①e12+e22= e12e22 ②e12+e22>4 ③e12+e22< e12e22 ④e12+e22>e12e22
其中正确的序号是_______
(理科)如下关于双曲线离心率的四个命题:
①如果相应于焦点F的准线与实轴相交于N,那么双曲线顶点分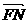 所成的比等于离心率e;
所成的比等于离心率e;
②当双曲线离心率越大时,它的开口就越开阔;③假定两个双曲线有共同渐近线时,则这两个双曲线的离心率相等;④若双曲线的一个焦点到一条渐近线的距离等于实半轴长,则此双曲线的离心率等于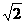 ,其中正确命题的序号是______
,其中正确命题的序号是______

 <x<0,sinx+cosx=
<x<0,sinx+cosx= ,
,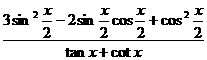 的值
的值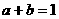 ,则
,则 的最大值为____________.
的最大值为____________.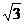 x+y=2
x+y=2