《2025年名校课堂八年级物理上册鲁科版五四制山东专版》

【例 1】星期天上午 9:00，小明骑车从家中出发前往相距 12 km 的外婆家，他先以 15 km/h 的速度骑行了 12 min，到达某一书店，在该书店买书用了 6 min，随后以 18 km/h 的速度骑行，按约定时间准时赶到外婆家(小明家、书店、外婆家大约在如图所示的直线上)。求：
(1)小明家到书店的距离。
(2)小明是几点几分到外婆家的。

答案：
(1)由$v = \frac{s}{t}$可得，小明家到书店的距离：
$s_1 = v_1t_1 = 15 km/h × \frac{12}{60} h = 3 km$
(2)书店到外婆家的距离：
$s_2 = s - s_1 = 12 km - 3 km = 9 km$
买书后骑车赶到外婆家所用的时间：
$t_2 = \frac{s_2}{v_2} = \frac{9 km}{18 km/h} = 0.5 h = 30 min$
小明从家到外婆家用的总时间：
$t_{总} = t_1 + t_0 + t_2 = 12 min + 6 min + 30 min = 48 min$
所以到达外婆家的时刻为$9:48$。

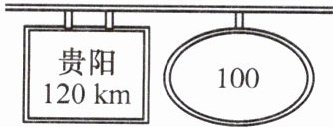
【例 2】小美一家回贵阳看望爷爷奶奶。汽车行驶了一段时间，她看到了如图所示的标志牌。在不违规的前提下，若汽车以最快的速度行驶，则从如图所示的标志牌到达贵阳时间是多少分钟？

答案： 由图可知，从标志牌到贵阳的路程$s = 120 km$，汽车的最大行驶速度$v = 100 km/h$，
由$v = \frac{s}{t}$可知，在不违规的前提下，若汽车以最快的速度行驶，从如图所示的标志牌到达贵阳时间：
$t = \frac{s}{v} = \frac{120 km}{100 km/h} = 1.2 h = 72 min$

【例 3】如图，南京长江大桥上层为公路桥，车行道宽 15 m，可容 4 辆大型汽车并行，两侧各有 2 m 多宽的人行道，大桥由正桥和引桥两部分组成，正桥 9 墩 10 跨，长 1 576 m。
(1)小明晚上步行到大桥上体验绚丽多彩的玉兰花灯，步行平均速度为 0.8 m/s，他通过正桥所用时间为多少？
(2)第二天小明全班同学前来参观大桥，排队匀速通过桥面。整个队伍长 44 m，整支队伍通过正桥正好用时 67.5 min，队伍行进的速度是多少？队伍全部在正桥上的时间是多少？

答案：
(1)他通过正桥所用时间：
$t = \frac{s}{v} = \frac{1576 m}{0.8 m/s} = 1970 s$
(2)队伍通过正桥所走的路程：
$s' = L_{桥} + L_{队伍} = 1576 m + 44 m = 1620 m$
队伍通过正桥的时间：
$t' = 67.5 min = 67.5 × 60 s = 4050 s$
队伍行进的速度：
$v' = \frac{s'}{t'} = \frac{1620 m}{4050 s} = 0.4 m/s$
队伍全部在正桥上的路程：
$s'' = L_{桥} - L_{队伍} = 1576 m - 44 m = 1532 m$
队伍全部在正桥上的时间：
$t'' = \frac{s''}{v} = \frac{1532 m}{0.4 m/s} = 3830 s$

【例 4】草原上正在进行着一场激烈的捕食战。野兔在草地上以 20 m/s 的速度向前方 100 m 处的树洞奔逃，同时秃鹰在野兔后方 110 m 处以 30 m/s 的速度贴着地面飞行追击野兔。通过计算判断野兔能否安全逃进树洞？

答案： 由$v = \frac{s}{t}$得，野兔跑到树洞所需时间：
$t_1 = \frac{s_1}{v_1} = \frac{100 m}{20 m/s} = 5 s$
秃鹰到洞口的路程：$s_2 = 100 m + 110 m = 210 m$
秃鹰到洞口所需的时间：
$t_2 = \frac{s_2}{v_2} = \frac{210 m}{30 m/s} = 7 s ＞ 5 s$
所以秃鹰到达洞口时，野兔能安全逃进树洞。