《2025年新课程课堂同步练习册七年级数学上册人教版》

2. 已知$\angle 1是\angle 2的2$倍,$\angle 1的余角的3倍与\angle 2$的补角相等,求$\angle 1$,$\angle 2$的度数.

答案： 设$\angle 2=x$,则$\angle 1=2x$,则$3(90° - 2x)=180° - x$,解得$x=18°$. 故$\angle 1=36°,\angle 2=18°$

3. 如图 6,$B$,$C是线段AD$上的两点,$E是线段AB$的中点,$F是线段CD$的中点,$AD = 18cm$,$BC = 5cm$.
(1)求$AB + CD$的长；
(2)求$E$,$F$两点之间的距离.

答案：
(1)$13\,cm$
(2)$11.5\,cm$

4. 如图 7,货轮$O$在航行过程中,发现灯塔$A在它的南偏东60^{\circ}$的方向上,同时,在它的北偏西$30^{\circ}$、西北方向上又发现了客轮$B和海岛C$.
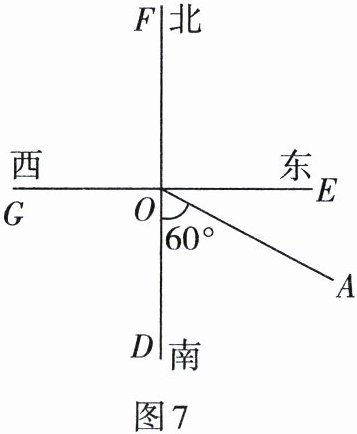
(1)仿照表示灯塔方位的方法,在图中画出表示客轮$B和海岛C$方向的射线；
(2)在(1)的条件下填空：$\angle BOC= $15°,$\angle BOE= $120°,和$\angle AOD$互余的角为：$\angle AOE$和$\angle BOF$.

答案：
(1)如右图所示
(2)$15°, 120°$,和$\angle AOD$互余的角为：$\angle AOE$和$\angle BOF$