《2025年状元成才路创优作业100分四年级数学上册人教版湖南专版》

1.



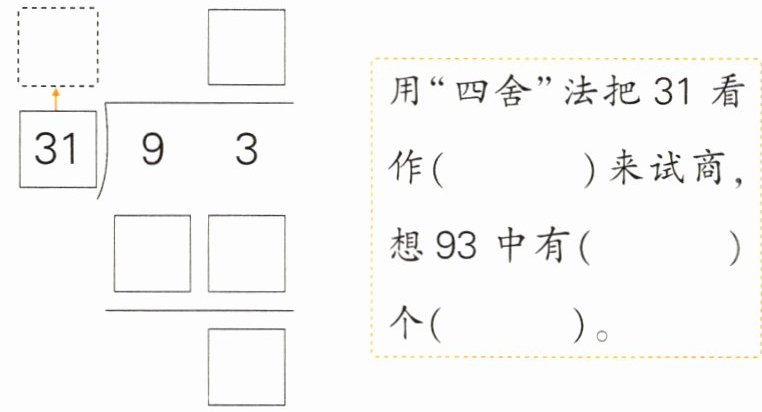
30　3　30　50　3　2

答案： 30　3　30　50　3　2

2. 根据试商情况,直接写出准确商。

准确商：(6) 准确商：(3)

答案： 6　3

3. 列竖式计算。
$72÷24= $ $358÷71= $
$100÷23= $ $408÷82= $

答案：

4. 小林用 207 个易拉罐进行 DIY 制作,制作笔筒用去了 15 个易拉罐,剩下的用来制作收纳箱,每 32 个易拉罐可以制作 1 个收纳箱,一共可以制作多少个收纳箱？

答案： (207 - 15)÷32=6(个)

5. 四年级的王老师要为班级图书角新购入一批儿童读物,每本 53 元。王老师的购书卡里原来有 36 元,如果再充值 400 元,最多能购买儿童读物多少本？

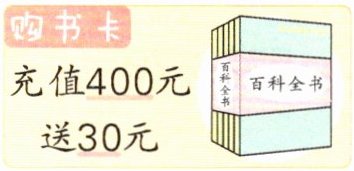
答案： 400+30+36=466(元)
466÷53=8(本)……42(元)

6. 在下面的$□$里填上合适的数,使商是一位数且没有余数。
$\begin{array}{r} \Box \\ 63\enclose{longdiv} {\Box \Box 4}\end{array}$　　　　　$\begin{array}{r} \Box \\ 91\enclose{longdiv} {3\Box \Box }\end{array}$
$\begin{array}{r} \boxed{8} \\ 63\enclose{longdiv} {\boxed{5}\boxed{0}4}\end{array}$　　　　　$\begin{array}{r} \boxed{4} \\ 91\enclose{longdiv} {3\boxed{6}\boxed{4}}\end{array}$

答案： 8　　　　　　　　　4
　63$\sqrt{504}$　　　　　91$\sqrt{364}$
[解析]要使□□4÷63的商是一位数且没有余数,则63乘一个一位数等于□□4,结果的末位是4,想3和几相乘的积的末位是4,3×8=24,此时商只能是8,再根据“被除数 = 除数×商”求出被除数即可。要使3□□÷91的商是一位数且没有余数,则91乘一个一位数等于3□□,想9乘几的积是三十多,9×4=36,当商为4时,91×4=364,符合条件。