《2025年初中同步学习目标与检测八年级数学上册人教版》

3. 如图,BP 平分∠ABC,PD⊥AB 于点 D,点 E 为射线 BC 上一点. 若 PD = 5,则 PE 的长度可能为( )

A.2
B.3
C.4
D.6

答案： D

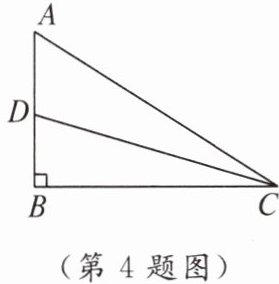
4. 如图,在 Rt△ABC 中,∠B = 90°,CD 平分∠ACB,AC = 4,BD = 1,则△ACD 的面积是______.

答案： 2

5. 如图,在 Rt△ABC 中,∠C = 90°,∠BAC 的平分线交 BC 于点 D,DE⊥AB 于 E. 若 BC = 9,AC = 12,AB = 15,则△BDE 的周长为( )

A.6
B.12
C.15
D.21

答案： B

6. 如图,AI,BI,CI 分别是∠BAC,∠ABC,∠ACB 的平分线,ID⊥BC,△ABC 的周长为 18,ID = 4,则△ABC 的面积为( )

A.18
B.30
C.36
D.72

答案： C

7. 如图,OE 平分∠AOB,点 F 在 OE 上,且 FA⊥OA,FD⊥OB,垂足分别为 A,D,FC = FB,判断 OB - OC 与 AC 有什么数量关系？并说明理由.

答案： 解 OB - OC=2AC,理由如下:
∵OE平分∠AOB,FA⊥OA,FD⊥OB,
∴∠AOF=∠DOF,∠FAC=∠FDO=∠FDB=90°,FA=FD.
在△FAO和△FDO中,$\left\{\begin{array}{l} ∠AOF=∠DOF,\\ ∠FAO=∠FDO,\\ OF=OF,\end{array}\right. $
∴△FAO≌△FDO(AAS),
∴OA=OD.
在Rt△FAC和Rt△FDB中,$\left\{\begin{array}{l} FC=FB,\\ FA=FD,\end{array}\right. $
∴Rt△FAC≌Rt△FDB(HL),
∴AC=BD,
∴OA=OD=OB - BD=OB - AC,OC=OA - AC,
∴OC=(OB - AC)-AC,
∴OB - OC=2AC.

2. 角的平分线的性质与判定的关系
$\begin{matrix}点在角的 & \xrightarrow{性质} & 点到角的两边 \\平分线上 & \xleftarrow{判定} & 的距离相等\end{matrix} $
点睛：角的平分线的性质是证两条线段相等的依据,角的平分线的判定是证两角相等的依据,在应用时不要混淆。

答案： 答题（以下为模拟答题卡中的作答内容）:
根据角的平分线的性质与判定的关系：
若点在角的平分线上，则该点到角的两边的距离相等（性质）；
若点到角的两边的距离相等，则该点在角的平分线上（判定）。
结论：
角的平分线的性质用于证明两条线段相等；
角的平分线的判定用于证明两角相等。