证明勾股定理的常用方法:将一个图形的
面积
用两种方法表示,一种是将图形看成一个整体进行表示,另一种是用组成图形的各部分之和表示,从而得到一个等式,再化简等式即可,这种方法叫作“算两次”。
答案:
面积
1. 在如图所示的图形中,能够验证勾股定理的有(
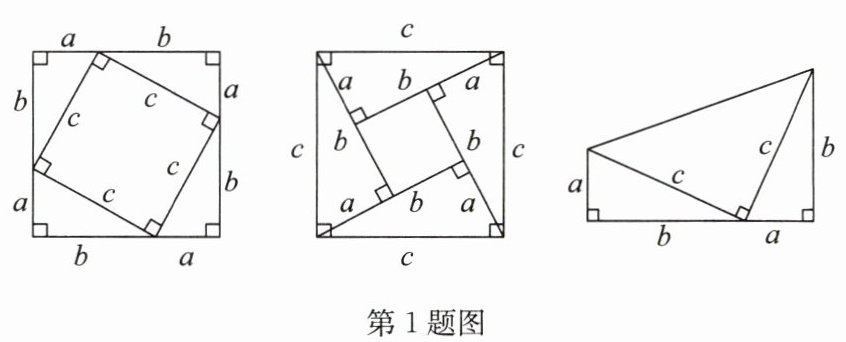
A.0 个
B.1 个
C.2 个
D.3 个
D
)
A.0 个
B.1 个
C.2 个
D.3 个
答案:
D
2. 若一个直角三角形的三边长分别为 2,3,x,则以 x 为边长的正方形的面积为(
A.5
B.13
C.5 或 13
D.4
C
)A.5
B.13
C.5 或 13
D.4
答案:
C
3. 若直角三角形一条直角边长为 6,斜边长为 10,则斜边上的高是(
A.$\frac{12}{5}$
B.$\frac{24}{5}$
C.5
D.6
B
)A.$\frac{12}{5}$
B.$\frac{24}{5}$
C.5
D.6
答案:
B
4. 如图,由 4 个相同的直角三角形拼成 2 个正方形,则 4 个直角三角形的面积+小正方形的面积= 大正方形的面积,即
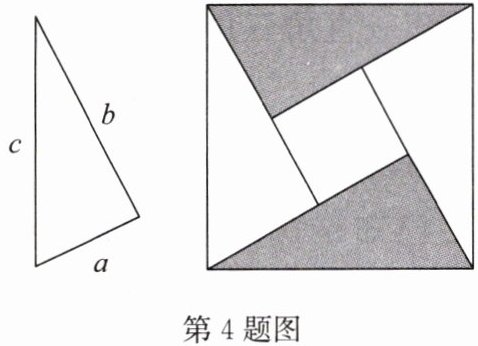
$4× \frac{1}{2}ab+(b-a)^2=c^2$
,化简得______$a^2+b^2=c^2$
。
答案:
$4× \frac{1}{2}ab+(b-a)^2=c^2$ $a^2+b^2=c^2$
5. 如图,在△ABC 中,AD⊥BC,AB= 15,AD= 12,AC= 13. 求 BC 的长.
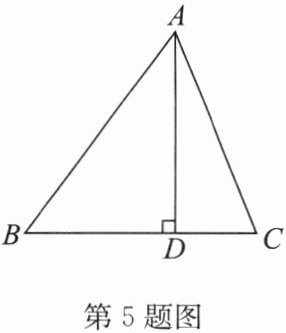

答案:
解:$\because AD\perp BC$,$\therefore \angle ADB=\angle ADC=90°$.
$\because AB=15$,$AD=12$,
$\therefore$在$Rt\triangle ABD$中,$BD^2=AB^2-AD^2=15^2-12^2=81$,
$\therefore BD=9$.
$\because AC=13$,$AD=12$,
$\therefore$在$Rt\triangle ACD$中,$CD^2=AC^2-AD^2=13^2-12^2=25$,
$\therefore CD=5$.$\therefore BC=BD+CD=9+5=14$.
$\because AB=15$,$AD=12$,
$\therefore$在$Rt\triangle ABD$中,$BD^2=AB^2-AD^2=15^2-12^2=81$,
$\therefore BD=9$.
$\because AC=13$,$AD=12$,
$\therefore$在$Rt\triangle ACD$中,$CD^2=AC^2-AD^2=13^2-12^2=25$,
$\therefore CD=5$.$\therefore BC=BD+CD=9+5=14$.
查看更多完整答案,请扫码查看


