1.
无限不循环小数
叫作无理数.无理数分为正
无理数和负
无理数.
答案:
无限不循环小数 正 负
2. ______数都可以写成分数形式$\frac{n}{m}$($m$,$n$是整数),______数不能写成分数形式$\frac{n}{m}$($m$,$n$是整数).
答案:
有理 无理
1. 下列四个数中,是无理数的是(
A.$\sqrt{4}$
B.$3.1415926$
C.$\frac{22}{7}$
D.$\sqrt{2}$
D
)A.$\sqrt{4}$
B.$3.1415926$
C.$\frac{22}{7}$
D.$\sqrt{2}$
答案:
D
2. 下列关于$\sqrt{10}$的说法,错误的是(
A.$\sqrt{10}$是无理数
B.$3<\sqrt{10}<4$
C.$10的平方根是\sqrt{10}$
D.$\sqrt{10}是10$的算术平方根
C
)A.$\sqrt{10}$是无理数
B.$3<\sqrt{10}<4$
C.$10的平方根是\sqrt{10}$
D.$\sqrt{10}是10$的算术平方根
答案:
C
3. 如图,数轴上的点$P$表示的无理数可能是(
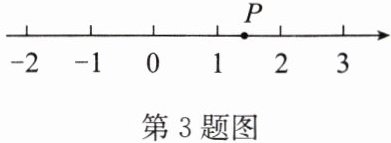
A.$\sqrt{2}$
B.$\sqrt{5}$
C.$\sqrt{6}$
D.$\pi$
A
)
A.$\sqrt{2}$
B.$\sqrt{5}$
C.$\sqrt{6}$
D.$\pi$
答案:
A
4. 设$a$,$b$是两个连续的整数,已知$\sqrt{8}$是一个无理数,若$a<\sqrt{8}<b$,则$a + b= $
5
.
答案:
5
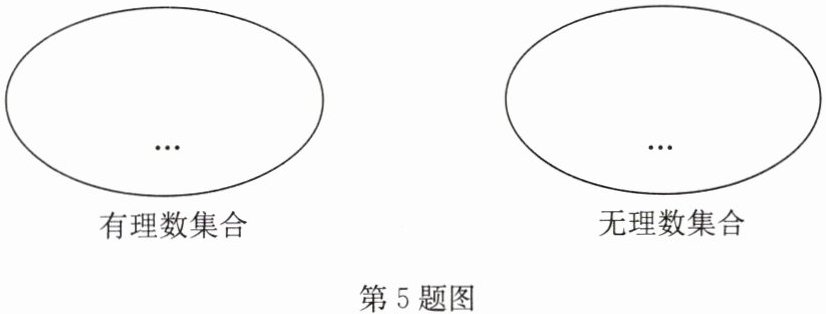
5. 如图,把下列各数分别填在相应的集合中.
$-\frac{11}{12}$,$\sqrt[3]{2}$,$\sqrt{4}$,$0$,$-\sqrt{0.4}$,$\sqrt[3]{8}$,$\frac{\pi}{4}$,$0.\dot{2}\dot{3}$,$3.14$.
$-\frac{11}{12}$,$\sqrt[3]{2}$,$\sqrt{4}$,$0$,$-\sqrt{0.4}$,$\sqrt[3]{8}$,$\frac{\pi}{4}$,$0.\dot{2}\dot{3}$,$3.14$.

答案:
解:如答图所示.
解:如答图所示.

6. 求$\sqrt{7}$的整数部分和小数部分.
答案:
解: $\because \sqrt{4} < \sqrt{7} < \sqrt{9}$, 即 $2 < \sqrt{7} < 3$, $\therefore \sqrt{7}$ 的整数部分为 2,小数部分为 $\sqrt{7}-2$.
查看更多完整答案,请扫码查看


