直角三角形的性质定理:直角三角形斜边上的中线等于
斜边的一半
.
答案:
斜边的一半
1. 如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A= 26°,则∠BDC的度数是(
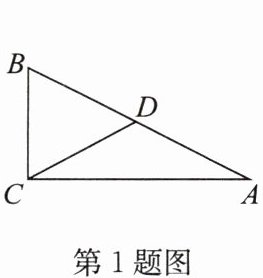
A.26°
B.38°
C.42°
D.52°
D
)
A.26°
B.38°
C.42°
D.52°
答案:
D
2. 如图,在Rt△ABC中,∠ACB= 90°,点D在AB边上,且∠DCA= ∠A,AB= 10,则CD的长为(
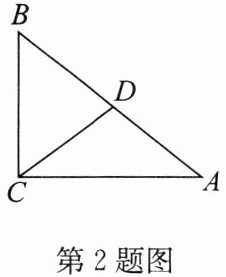
A.4
B.4.5
C.5
D.6
C
)
A.4
B.4.5
C.5
D.6
答案:
C
3. 如图,在Rt△BAC和Rt△BDC中,∠BAC= ∠BDC= 90°,O是BC的中点,连接AO,DO. 若AO= 3,则DO的长为
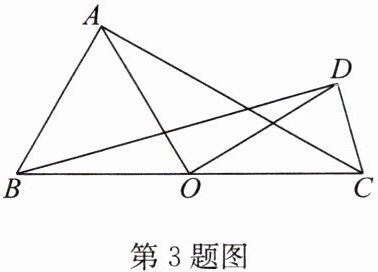
3
.
答案:
3
4. 若一个直角三角形斜边上的高和中线的长分别是4 cm,6 cm,则这个直角三角形的面积是
24
$cm^2.$
答案:
24
5. 如图,OP平分∠MON,A为OM上的一点,AH⊥OP于点H,B是AO的中点,求证:BH//ON.
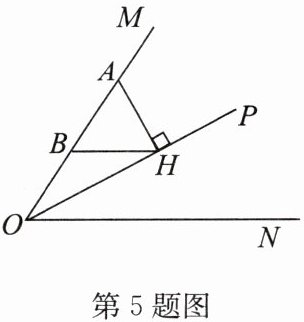

答案:
证明:
∵AH⊥OP,B是AO的中点,
∴BH=$\frac{1}{2}$OA=OB,
∴∠BOH=∠BHO.
∵OP平分∠MON,
∴∠BOH=∠NOP,
∴∠BHO=∠NOP,
∴BH//ON.
∵AH⊥OP,B是AO的中点,
∴BH=$\frac{1}{2}$OA=OB,
∴∠BOH=∠BHO.
∵OP平分∠MON,
∴∠BOH=∠NOP,
∴∠BHO=∠NOP,
∴BH//ON.
查看更多完整答案,请扫码查看


