1. 有
两条边
相等的三角形叫作等腰三角形,相等的边叫作腰
.
答案:
两条边 腰
2. 等腰三角形的性质定理 1:等腰三角形的
两底角
相等(简称“等边对等角
”).
答案:
两底角 等边对等角
3. 等腰三角形的性质定理 2:等腰三角形
底边上的高线
、______中线
及______顶角平分线
重合(简称“______三线合一
”).
答案:
底边上的高线 中线 顶角平分线 三线合一
4. 等腰三角形是轴对称图形,
底边的垂直平分线
是它的对称轴.
答案:
底边的垂直平分线
1. 等腰三角形的顶角是 $50^{\circ}$,则这个三角形的一个底角的度数是(
A.$65^{\circ}$
B.$40^{\circ}$
C.$50^{\circ}$
D.$80^{\circ}$
A
)A.$65^{\circ}$
B.$40^{\circ}$
C.$50^{\circ}$
D.$80^{\circ}$
答案:
A
2. 如图,在$\triangle ABC$中,$AB = AC$,$AD\perp BC$,且 $BC = 4$,则 $BD$ 的长为(
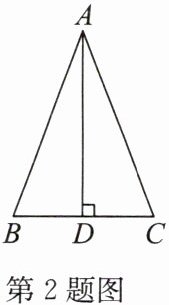
A.$1$
B.$2$
C.$3$
D.$4$
B
)
A.$1$
B.$2$
C.$3$
D.$4$
答案:
B
3. 等腰三角形的一个外角是 $130^{\circ}$,则它的底角是(
A.$50^{\circ}$
B.$80^{\circ}$
C.$50^{\circ}$或 $80^{\circ}$
D.$50^{\circ}$或 $65^{\circ}$
D
)A.$50^{\circ}$
B.$80^{\circ}$
C.$50^{\circ}$或 $80^{\circ}$
D.$50^{\circ}$或 $65^{\circ}$
答案:
D
4. 如图,在$\triangle ABC$中,$D$ 是边 $BC$ 上的一点,$AB = AD = DC$,$\angle C = 35^{\circ}$,求$\angle B$ 和$\angle DAC$的度数.
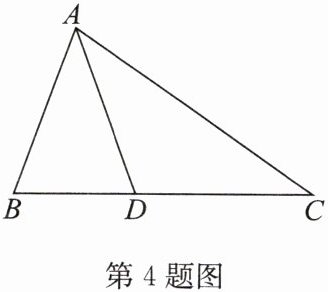

答案:
解:
∵AD=DC,∠C=35°,
∴∠DAC=∠C=35°.
∴∠ADB=∠DAC+∠C=70°.
∵AB=AD,
∴∠B=∠ADB=70°.
∵AD=DC,∠C=35°,
∴∠DAC=∠C=35°.
∴∠ADB=∠DAC+∠C=70°.
∵AB=AD,
∴∠B=∠ADB=70°.
5. 如图,在$\triangle ABC$中,$AB = AC$,$AD// CB$,求证:$AD$ 平分$\angle CAE$.
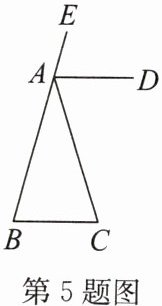

答案:
证明:
∵在△ABC中,AB=AC,
∴∠B=∠C.
∵AD//CB,
∴∠B=∠EAD,∠C=∠CAD,
∴∠EAD=∠CAD,
∴AD平分∠CAE.
∵在△ABC中,AB=AC,
∴∠B=∠C.
∵AD//CB,
∴∠B=∠EAD,∠C=∠CAD,
∴∠EAD=∠CAD,
∴AD平分∠CAE.
查看更多完整答案,请扫码查看


