《2025年启东中学作业本八年级数学上册苏科版宿迁专版》

勾股定理(也被称为毕达哥拉斯定理):直角三角形两条直角边的平方和等于斜边的平方,即直角三角形的两条直角边$a,b与斜边c$之间满足:$a^{2}+b^{2}=c^{2}$.

答案： 毕达哥拉斯定理 斜边的平方 $a^{2}+b^{2}=c^{2}$

1. 在$\triangle ABC$中,$\angle A,\angle B,\angle C的对边长分别为a,b,c$,若$\angle A+\angle C= 90^{\circ}$,则下列等式中成立的是(C)
A.$a^{2}+b^{2}= c^{2}$
B.$b^{2}+c^{2}= a^{2}$
C.$a^{2}+c^{2}= b^{2}$
D.$(c+a)^{2}= b^{2}$

答案： C

2. 已知一直角三角形木板三边的平方和为$1800\ cm^{2}$,则斜边长为(B)
A.$80\ cm$
B.$30\ cm$
C.$90\ cm$
D.$120\ cm$

答案： B

3. 下列说法正确的是(C)

A.已知$a,b,c$是三角形的三边长,则$a^{2}+b^{2}= c^{2}$
B.在直角三角形中,两边的平方和等于第三边的平方
C.在$Rt\triangle ABC$中,$\angle A,\angle B,\angle C的对边长分别为a,b,c,\angle C= 90^{\circ}$,所以$a^{2}+b^{2}= c^{2}$
D.在$Rt\triangle ABC$中,$\angle A,\angle B,\angle C的对边长分别为a,b,c,\angle B= 90^{\circ}$,所以$a^{2}+b^{2}= c^{2}$

答案： C

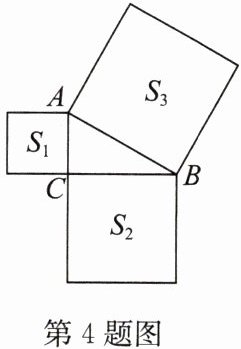
4. 如图,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,以它的各边为边向外作三个正方形,面积分别为$S_{1},S_{2},S_{3}$,已知$S_{1}= 6,S_{2}= 8$,则$S_{3}= $14.

答案： 14

5. 若一等腰三角形的腰长为$10$,底边长为$12$,则底边上的高为8.

答案： 8

6. 设直角三角形的两条直角边长分别为$a和b$,斜边长为$c$.
(1)已知$a = 12,b = 5$,求$c$的值；
(2)已知$a = 3,c = 5$,求$b$的值；
(3)已知$c = 15,b = 9$,求$a$的值.

答案： 解:
(1)
∵直角三角形的两条直角边长分别为a和b,斜边长为c,a=12,b=5,
$\therefore c^{2}=a^{2}+b^{2}=12^{2}+5^{2}=169,\therefore c=13.$
(2)
∵直角三角形的两条直角边长分别为a和b,斜边长为c,a=3,c=5,$\therefore b^{2}=c^{2}-a^{2}=5^{2}-3^{2}=16,\therefore b=4.$
(3)
∵直角三角形的两条直角边长分别为a和b,斜边长为c,c=15,b=9,$\therefore a^{2}=c^{2}-b^{2}=15^{2}-9^{2}=144,\therefore a=12.$