《2025年伴你学江苏九年级物理上册苏科版》

9. 起重机将 1 000 N 的重物竖直向上匀速提升 15 m 后,又将重物水平匀速移动了 5 m,整个过程中,竖直向上的拉力对重物做功1.5×10⁴J。

答案： 1. 首先分析做功的条件：
根据功的计算公式$W = Fs$（其中$F$是力，$s$是在力的方向上移动的距离）。
当起重机竖直向上提升重物时，拉力$F = G=1000N$（因为重物匀速运动，拉力与重力平衡），在竖直方向上移动的距离$s_1 = 15m$。
当重物水平匀速移动时，拉力方向竖直向上，水平移动的距离$s_2 = 5m$，在拉力方向上没有移动距离（力与距离方向垂直），此过程拉力不做功。
2. 然后计算竖直提升重物时拉力做的功：
把$F = 1000N$，$s_1 = 15m$代入$W = Fs$，可得$W=Fs_1$。
$W = 1000N×15m=15000J$。
故答案为：$15000$。

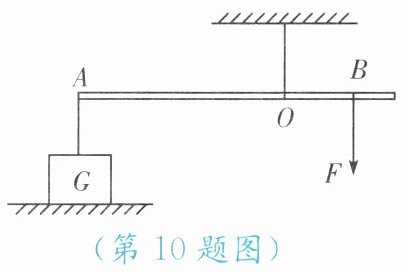
10. 轻质木杆 AB 可以绕点 O 转动,OA∶OB＝3∶1,A 端挂有重力为 300 N 的重物,重物静止在水平地面上。若要使木杆保持水平,且重物对水平地面的压力为零,则需在 B 端用900N 的力竖直向下拉。此时木杆为费力(选填“省力”“费力”或“等臂”)杠杆。

答案： 900
费力

11. 我国自行研制的歼 - 20 战斗机的质量为$ 1.7×10^4 kg,$设发动机用$ 1.4×10^5 N $的推力使飞机在 10 s 内前进了 5 000 m。飞机受到的重力为$1.7×10^5$N,这段时间内飞机的平均速度为500m/s,推力的功率为$7×10^7$W。(g 取 10 N/kg)

答案： 1. 首先求飞机受到的重力：
根据重力公式$G = mg$（其中$m = 1.7×10^{4}kg$，$g = 10N/kg$）。
则$G=mg = 1.7×10^{4}kg×10N/kg=1.7×10^{5}N$。
2. 然后求飞机的平均速度：
根据平均速度公式$v=\frac{s}{t}$（其中$s = 5000m$，$t = 10s$）。
则$v=\frac{s}{t}=\frac{5000m}{10s}=500m/s$。
3. 最后求推力的功率：
先根据$W = Fs$（其中$F = 1.4×10^{5}N$，$s = 5000m$）求出推力做的功，$W = Fs=1.4×10^{5}N×5000m = 7×10^{8}J$。
再根据功率公式$P=\frac{W}{t}$（其中$W = 7×10^{8}J$，$t = 10s$）。
则$P=\frac{W}{t}=\frac{7×10^{8}J}{10s}=7×10^{7}W$。
故答案依次为：$1.7×10^{5}$；$500$；$7×10^{7}$。

12. 如图所示,物体 A 重为 16 N,手拉绳的力为 10 N。当物体被匀速提升高度 h 时,动滑轮的机械效率为80%(不考虑摩擦)。若想增大动滑轮的机械效率,可采用的方法是减小动滑轮重(写出一种即可)。

答案： 80%
减小动滑轮重

13. 如图所示,在测定杠杆机械效率的实验中,竖直向上匀速拉动弹簧测力计,使挂在杠杆 OB 上的物块缓慢上升至虚线位置,弹簧测力计的示数 F 为 2.5 N,弹簧测力计竖直移动的距离 s 为 0.2 m。物块重为 1.5 N,物块上升的高度 h 为 0.3 m,则杠杆的机械效率为90%,使用杠杆提升物块的过程中,需做额外功的原因之一是要克服杠杆自身重力做功。

答案： 1. 首先计算有用功$W_{有}$：
根据公式$W_{有}=Gh$（其中$G$是物块重力，$h$是物块上升高度），已知$G = 1.5N$，$h = 0.3m$，则$W_{有}=Gh=1.5N×0.3m = 0.45J$。
2. 然后计算总功$W_{总}$：
根据公式$W_{总}=Fs$（其中$F$是弹簧测力计示数，$s$是弹簧测力计移动距离），已知$F = 2.5N$，$s = 0.2m$，则$W_{总}=Fs=2.5N×0.2m = 0.5J$。
3. 最后计算杠杆的机械效率$\eta$：
根据机械效率公式$\eta=\frac{W_{有}}{W_{总}}×100\%$，将$W_{有}=0.45J$，$W_{总}=0.5J$代入可得：$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{0.45J}{0.5J}×100\% = 90\%$。
使用杠杆提升物块的过程中，需做额外功的原因之一是：要克服杠杆自身重力做功（或杠杆与支点$O$处有摩擦）。
故答案依次为：$90\%$；要克服杠杆自身重力做功（或杠杆与支点$O$处有摩擦）。

14. 如图所示,用大小为 2.5 N 的拉力 F 沿斜面将重 5 N 的小车从点 A 拉到点 B。测得 A、B 两点间的距离 s＝50 cm,点 A 距地面的高度$ h_1＝5 cm,$点 B 距地面的高度$ h_2＝25 cm。$由此可知,拉力 F 做的功是1.25J,其中克服摩擦力做的功是0.25J,摩擦力是0.5N,斜面的机械效率是80%。若斜面完全没有摩擦,则至少需要2N 的拉力才能拉动小车。

答案： 1. 计算拉力$F$做的功：
根据公式$W = Fs$，已知$F = 2.5N$，$s = 50cm=0.5m$。
则$W_{总}=Fs = 2.5N×0.5m = 1.25J$。
2. 计算有用功：
根据公式$W_{有}=G\Delta h=G(h_{2}-h_{1})$，已知$G = 5N$，$h_{1}=5cm = 0.05m$，$h_{2}=25cm = 0.25m$。
则$W_{有}=G(h_{2}-h_{1})=5N×(0.25m - 0.05m)=1J$。
3. 计算克服摩擦力做的功：
因为$W_{总}=W_{有}+W_{额}$，所以$W_{额}=W_{总}-W_{有}$。
$W_{额}=1.25J - 1J = 0.25J$。
4. 计算摩擦力：
又因为$W_{额}=fs$，所以$f=\frac{W_{额}}{s}$。
已知$W_{额}=0.25J$，$s = 0.5m$，则$f=\frac{0.25J}{0.5m}=0.5N$。
5. 计算斜面的机械效率：
根据公式$\eta=\frac{W_{有}}{W_{总}}×100\%$。
则$\eta=\frac{1J}{1.25J}×100\% = 80\%$。
6. 若斜面完全没有摩擦，计算拉力：
此时$W_{总}=W_{有}$，即$F's = G(h_{2}-h_{1})$。
则$F'=\frac{G(h_{2}-h_{1})}{s}$，把$G = 5N$，$h_{2}-h_{1}=0.2m$，$s = 0.5m$代入。
$F'=\frac{5N×0.2m}{0.5m}=2N$。
故答案依次为：$1.25$；$0.25$；$0.5$；$80\%$；$2$。

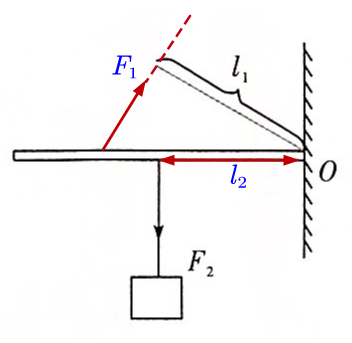
15. 如图所示,杠杆在力$ F_1、$$F_2$作用下处于平衡状态$,l_1$为$ F_1$的力臂。请在图中作出$ F_2$的力臂$ l_2$及力$ F_1。$

答案：