《2025年新课程问题解决导学方案八年级物理上册人教版》

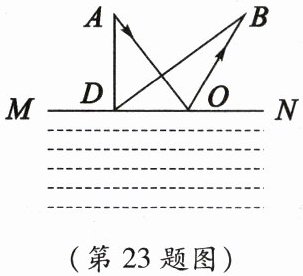
23. 如图所示,A、B两地相距4 km,MN是与AB连线平行的一条小河的河岸,A、B两地到河岸的垂直距离均为3 km,小军要从A地走到河岸取水然后送到B地,他先沿垂直于河岸的方向到D点取水,再沿直线DB到B地。若小军的速度大小恒为5 km/h,不考虑取水停留的时间。

(1)求小军完成这次取水和送水任务所需要的总时间。
(2)为了找到一条最短路线(即从A地到河岸和从河岸到B地的总路程最短),可以将MN看成一个平面镜,从A地作出一条光线,经MN反射后恰能通过B地。请你证明入射点O为最短路线的取水点。

答案：

(1)解:s=AD+DB
=3km+5km
=8km,
由$ v=\frac{s}{t} $得，所需的总时间
$ t=\frac{s}{v}=\frac{8\ km}{5\ km/h}=1.6\ h $。
(2)如图，根据平面镜成像的特点，作出A 地关于MN的对称点A',连接A'B,与MN相交于O点，连接AO,则A'O=AO,故取水点为O点时的路线长度s=AO+OB=A'O+OB=A'B。在O 点以外的河岸上任取一点P,路线的长度s'=AP+PB=A'P+PB。由三角形知识可知A'B＜A'P+PB,即s＜s',故入射点O为最短路线的取水点。