第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
3. 填一填。
(1)将一个圆平均分成若干等份,可以拼成一个近似的平行四边形,这个平行四边形的底相当于圆的(
(2)一个圆的半径是$3cm$,周长是(
(3)一个圆内最长的线段长$8dm$,这个圆的面积是(
(4)如果用一根$21.98cm$的绳子正好围了一个圆形,那么这个圆的面积是(
(1)将一个圆平均分成若干等份,可以拼成一个近似的平行四边形,这个平行四边形的底相当于圆的(
周长的一半
),高相当于圆的(半径
)。因为平行四边形面积等于(底×高
),所以圆形面积等于(周长的一半×半径
),用字母表示为$S=$(πr²
)。(2)一个圆的半径是$3cm$,周长是(
18.84
)$cm$,面积是(28.26
)$cm^{2}$。(3)一个圆内最长的线段长$8dm$,这个圆的面积是(
50.24
)$dm^{2}$。(4)如果用一根$21.98cm$的绳子正好围了一个圆形,那么这个圆的面积是(
38.465
)$cm^{2}$。
答案:
(1) 周长的一半,半径,底×高,周长的一半×半径,πr²
(2) 18.84,28.26
(3) 50.24
(4) 38.465
(1) 周长的一半,半径,底×高,周长的一半×半径,πr²
(2) 18.84,28.26
(3) 50.24
(4) 38.465
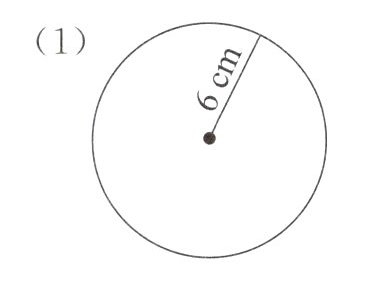
4. 计算各圆的面积。


答案:
(1)
根据圆的面积公式$S = \pi r^{2}$(其中$S$表示圆的面积,$\pi$通常取$3.14$,$r$为圆的半径)。
已知该圆半径$r = 6cm$,则其面积$S=3.14×6^{2}=3.14×36 = 113.04cm^{2}$。
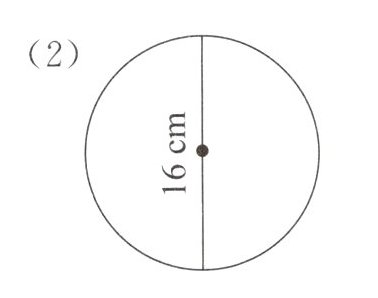
(2)
由图可知圆的直径为$16cm$,那么半径$r = 16÷2 = 8cm$。
根据圆的面积公式$S = \pi r^{2}$,$\pi$取$3.14$,可得该圆面积$S = 3.14×8^{2}=3.14×64 = 200.96cm^{2}$。
综上,答案依次为:
(1)$113.04cm^{2}$;
(2)$200.96cm^{2}$。
(1)
根据圆的面积公式$S = \pi r^{2}$(其中$S$表示圆的面积,$\pi$通常取$3.14$,$r$为圆的半径)。
已知该圆半径$r = 6cm$,则其面积$S=3.14×6^{2}=3.14×36 = 113.04cm^{2}$。
(2)
由图可知圆的直径为$16cm$,那么半径$r = 16÷2 = 8cm$。
根据圆的面积公式$S = \pi r^{2}$,$\pi$取$3.14$,可得该圆面积$S = 3.14×8^{2}=3.14×64 = 200.96cm^{2}$。
综上,答案依次为:
(1)$113.04cm^{2}$;
(2)$200.96cm^{2}$。
5. 如图,把一张圆形纸片平均剪成$32$份,剪下后,拼成一个近似的平行四边形,已知平行四边形的底是$12.56cm$,这个圆的周长是(

25.12
)$cm$。
答案:
25.12
6. 按要求画一画,并简要说一说画的过程。
(1)在正方形内画一个最大的圆。

(2)在正方形外面画一个圆,要求正方形的四个顶点都在圆上。

(1)在正方形内画一个最大的圆。

(2)在正方形外面画一个圆,要求正方形的四个顶点都在圆上。

答案:
(1) 画正方形两条对角线,交点为圆心;以圆心到正方形边的距离为半径画圆。

(2) 画正方形两条对角线,交点为圆心;以圆心到正方形顶点的距离为半径画圆。

(1) 画正方形两条对角线,交点为圆心;以圆心到正方形边的距离为半径画圆。

(2) 画正方形两条对角线,交点为圆心;以圆心到正方形顶点的距离为半径画圆。

查看更多完整答案,请扫码查看


